| 힙과 힙정렬 - 2 |
아래의 글에 이어지는 글입니다.
[강의노트] 힙과 힙정렬 - 1
힙과 힙정렬 힙이란? 내부노드에 키를 저장하며 다음 두가지 속성을 만족하는 이진트리 ( 외부노드에는 키를 저장하지 않는다는 것 .) 힙순서(heap-order): 루트를 제외한 모든 내부노드 v에 대해, ke
man-25-1.tistory.com
배열에 기초한 힙 구현
이미 지난 실습에서 우리는 배열을 이용해서 힙을 생성하는 코드를 작성해보았다.
https://man-25-1.tistory.com/154?category=938895
[실습] 삽입식 힙 생성
삽입식 힙 생성 포스트에 게시된 것은 알고리즘 수업자료에 대한 기록입니다. 제가 작성한 소스코드에 대한 카피를 금지합니다. 힙은 이진트리로 구현된 우선순위 큐다. 여기서 이진트리를 배
man-25-1.tistory.com
그 내용을 좀 더 formal 하게 정리해보자.
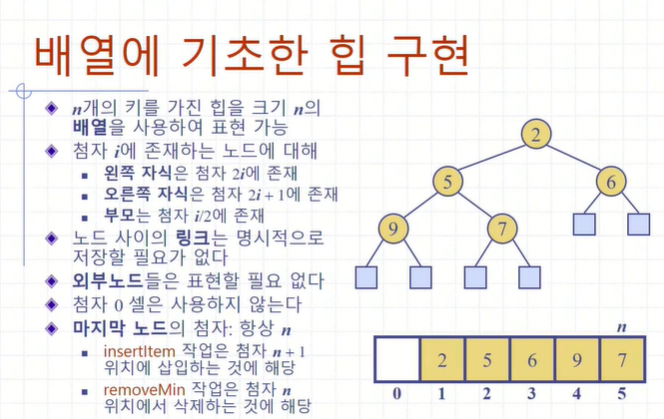
지난 실습에서 프로그래밍 조건에 배열의 인덱스 0번은 사용하지않는다. 라는 조건이 있었다.
| 배열에 기초한 힙을 구현할 때, 0번 인덱스를 사용하지않는 이유 현재 노드의 인덱스가 i 라고 할 때, 부모노드의 인덱스: 2/i 왼쪽 자식노드 : 2 * i 오른쪽 자식노드 : 2 * i +1 와 같이 표현할 수 있다. 하지만 0번 인덱스부터 채워넣게되면 위와 같은 공식이 성립하지 않으므로 편의를 위해서 0번 인덱스를 사용하지 않는다. |
또 배열을 가지고 힙을 구현할 때, 바로 이전 포스팅의 마지막 부분에서 다루었던 마지막 노드의 갱신 알고리즘이
매우 간단해지는 것을 확인할 수 있다.
배열에서는 마지막 노드의 위치를 n으로 두고, n에 단순히 1을 더하고 빼는 과정으로 갱신할 수 있기때문.
이런 차이점 때문에, 연결힙과 순차힙에서는 마지막 노드의 갱신에 대한 알고리즘에서 차이가 난다.

힙 정렬
지금까지 열심히 배운 힙 , 그리고 관련 메소드들을 활용해서 정렬을 해보자.

주목할만한 몇가지를 살펴보자.
힙정렬의 시간 복잡도는 O(n* log n)이다. 즉 O(n^2)의 선택정렬이나 삽입정렬보다 훨씬 빠르게 정렬할 수 있다.
어떻게 O(n * log n)의 속도로 정렬을 수행할 수 있는지 수도코드를 살펴보자.
| Alg heapSort(L) input list L output sorted list L 1. H <- empty heap # 비어있는 힙 생성 2. while (!L.isEmpty()) #리스트가 비워질때까지 반복 k <- L.removeFirst() # 리스트의 첫번째 원소를 힙에 삽입( 즉 while 안에서 n번 반복하게 됨) H.insertItem(k) # insertItem은 O(log n) * n번 반복 ==> O ( n * log n) 3. while (!H.isEmpty()) k <- H.removeMin() #최소힙에서 루트제거 L.addLast(k) # 최솟값이 리스트에 삽입 4. return # 결과 리스트가 오름차순으로 정렬된다 |
먼저 첫번째 페이즈부터 살펴보자.
| 2. while (!L.isEmpty()) k <- L.removeFirst() H.insertItem(k) phase 1 에 해당하는 while문은 삽입식 힙 생성을 나타낸다. 무순리스트의 원소들을 힙에 하나씩 삽입하면서 힙을 생성한다. 이때 시간복잡도는 리스트에서 첫번째 원소를 삭제하는 작업을 n번 반복해서 O( 1 * n ) insertItem 알고리즘을 n번 반복해서 O( n * log n) 이 걸리는데 O(n) < O(n*logn) 이므로, 첫번째 페이즈의 시간복잡도는 O(n*logn)이다. |
다음 페이즈가 힙 정렬에 해당한다.
| 3. while (!H.isEmpty()) k <- H.removeMin() #최소힙에서 루트제거 L.addLast(k) # 최솟값이 리스트에 삽입 힙에 있는 최솟값을 빼내서, 1번 페이즈에서 비워진 리스트에 삽입하는 과정이다. 이 과정에서 정렬이 이루어지게 된다 시간복잡도를 생각해보자. 힙에서 최솟값을 꺼내는 것은 O(log n)의 시간이 걸리고, 힙이 비워질때까지 반복하므로 O( n *log n) 리스트에 k를 삽입하는 것은 O( 1 * n )이다. 첫번째 페이즈와 마찬가지로 O(n) < O(n*logn) 이므로, 두번째 페이즈의 시간복잡도 역시 O(n*logn)이다. |
힙 정렬 개선
위의 정렬 알고리즘은 두가지 관점에서 개선방향이 존재한다
1. 처음 입력으로 주어진 리스트 L 외에 새로운 공간인 H를 사용했다. H를 사용하지않고 제자리 힙 정렬을 수행할 수 있다면 heap sort의 메모리(공간) 사용을 줄일 수 있을 것이다.
(원래 주어진 제 1공간인 L 만 가지고도 정렬이 가능하다)
2. 상향식 힙 생성은 O(n)의 시간에서 동작하기때문에 heap sort의 속도를 높혀줄 수 있을 것이다.
( 1번 페이즈의 힙 생성과정에서 삽입식 힙 생성이 아닌 상향식 힙 생성으로 진행하면, 속도가 향상된다)
1. 제자리 힙 정렬
먼저 제자리 힙 정렬에 대해서 알아보자.
- 이 방식은 정렬되어야 할 리스트가 배열로 주어진 경우에만 적용가능하다
- 힙을 저장할 때 리스트 L의 일부를 사용함으로써 외부 힙 사용(즉 추가적인 메모리 사용)을 피한다.
- 지금까지 사용했던 최소힙 대신 최대힙을 사용한다.( 오름차순 정렬을 위해 )

제자리정렬의 inPlaceHeapSort 알고리즘을 보면, 위에서 다루었던 힙정렬과 마찬가지로
힙 생성에 해당하는 페이즈 1 과 힙 정렬에 해당하는 phase 2 로 구성되어있다.
먼저 페이즈 1에 해당하는 buildHeap 알고리즘을 살펴보자.
| Alg buildHeap(A) input array A of n keys output heap A of size n 1. for i <- 1 to n insertItem(A[i]) 2. return |
순차힙에서 insertItem 은 O(logn) 이므로 n번 반복해서 O(n *logn)이다.
따라서 페이즈1 ( 힙 생성)은 O(n *log n)의 시간복잡도를 가진다.
다음은 페이즈 2에서 정렬알고리즘을 살펴보자.
| for i <- n downto 2 A[1] <-> A[i] downHeap(1,i - 1) return Alg downHeap(i,last) input index i of array A representing a maxheap of size last output none 1. left <- 2i 2. right <- 2i + 1 3. if(left > last) return 4. greater <- left 5. if ( right <= last) if(key(A[right]) > key(A[greater])) greater <- right 6. if( keyA[i]) >= key(A[greater])) return 7. A[i] <-> A[greater] 8. downHeap(greater,last) |
for문에서 n부터 2까지 감소하며
A[1] <-> A[i]
downHeap(1,i-1) 을 수행한다.
힙을 생성하고, 정렬하는 두 종류의 구성은 동일하다. 근데 외부공간을 사용하지않고 위의 알고리즘이 구현가능하다고?
의문이 생긴다.
내 실력으로는 위의 코드만 보아서는 이해가 어렵다.
그림을 통해 이해해보자.

위의 그림을 보면, 리스트가 파란색 공간과 노란색 공간으로 나뉘어져있다.
앞의 파란색 공간이 heap 에 해당하는데, 실제 코드로 나타나는 것이 아닌 프로그래머의 마음속에 존재하는 가상의 공간이다. 노란색공간은 실제 코드로 존재하는 list를 의미한다.
그림은 phase1의 힙 생성 과정 중에 한 장면을 캡쳐한 것이다.
처음 시작에서는 list의 모든 원소가 노란색으로 채워져있었을 것이다. ( 가상의 힙이 비워진 상태 )

phase 1 , 힙 생성에서는 리스트의 경계를 왼쪽에서 오른쪽으로 한번에 한칸씩 이동한다.
즉 가상의 힙 공간(그림에서 파란색 공간)을 하나씩 늘려주는 것이다.
phase 2 , 힙 정렬에서는 힙이 생성되고, 리스트는 비워지게 된다. ( 모든 공간이 파란색 공간으로 될 것이다.)
이때 경계를 오른쪽에서 왼쪽으로 이동하면서, 힙의 최대 원소를 삭제하며 리스트 인덱스 i에 저장한다.
최종 정렬 결과는 힙이 모두 삭제되고 정렬된 리스트가 존재하게 될 것이다.
아래는 상세 예시가 나와있다.
무순 리스트 4,7,3,5,9,1 가 존재한다고 가정하자. 현재 파란색 공간에 해당하는 힙은 비워져있고
노란색 공간에 해당하는 리스트만 존재한다.
이때 경계를 왼쪽에서 오른쪽으로 한칸 이동해서 4를 가상의 힙에 넣는다. 이것이 그림의 1단계이다.
또 한칸 이동해서 7을 힙에 넣는다. heap 구조에서는 최대 값이 루트노드에 위치해야하므로 heapify가 수행될 것이다.
그 결과 2단계에서 7,4 // 3,5,9,1이 된다.
3단계도 마찬가지이다.

4단계 5단계 또한 위와 마찬가지로 작업이 수행된다.

6단계를 통해 phase 1 힙 생성 단계가 끝이 났다.
기존의 무순 리스트가 비워지고 최대 힙으로 변환되었다.
이때 힙이 생성되는 과정속에서 외부공간이 사용되지 않았다는 점에 주목하자.

이제 2기, 힙 정렬을 수행할 차례이다.
최대힙 구조에서 최대값을 삭제하면서 정렬된 리스트를 만들어야한다.
이번에는 경계를 오른쪽에서 왼쪽으로 한칸씩 이동하면서 최대값에 해당하는 값을 리스트에 삽입한다.



그림을 통해 이해하니 쉽게 이해할 수 있었다.
참고사항%%
비어있는 트리의 모습은 외부노드가 하나 있을때이다.
'지난 학기들의 기록 > 알고리즘' 카테고리의 다른 글
| [강의노트] 합병정렬과 퀵정렬 - 1 (2) | 2021.09.29 |
|---|---|
| [강의노트] 힙과 힙정렬 - 3 (0) | 2021.09.25 |
| [실습] 상향식 힙 생성 (0) | 2021.09.07 |
| [강의노트] 힙과 힙정렬 - 1 (0) | 2021.09.06 |
| [실습] 삽입식 힙 생성 (0) | 2021.09.05 |




댓글