| 합병정렬과 퀵정렬 |
합병정렬과 퀵정렬에 대한 강의 노트입니다.
분할통치법
합병정렬에 대해 알아보기전에 먼저 분할통치법의 개념에 대해 알아보자.
쉽게 말해서 큰 문제를 작은 문제로 나누어서 해결하고, 그것을 합쳐서 큰 문제를 해결하는 것이다.
1. 분할 : 입력 데이터 L을 둘 이상의 분리된 부분집합 L1,L2, . . .으로 나눈다.
( 큰 문제를 작은 문제로 분할)
2. 재귀 : L1,L2, ... 로 나눠진 작은 문제를 재귀적으로 해결한다.
3. 통치 : 해결을 합쳐서 전체 문제 L에 대한 해결법을 구한다.

위의 1,2,3번을 그대로 정렬에 사용한 알고리즘이 합병정렬이다.
합병정렬
위의 1,2,3번을 그대로 정렬에 사용한 알고리즘이 합병정렬이다. 분할통치법에 기초한 정렬 알고리즘.
힙정렬 vs 합병정렬.
힙정렬처럼 비교에 기초한 정렬이고 O(n*log n) 시간에 수행가능하다.
하지만 힙정렬과 다르게 외부의 우선순위 큐를 사용하지 않는다.
데이터를 순차적 방식으로 접근 ( 따라서 디스크의 데이터를 정렬하기에 적당하다 )

그럼 구체적으로 합병 정렬은 어떤 알고리즘으로 구현될까?
1. 분할 단계에서는 무순 리스트 L을 작은 부리스트로 나눈다.
이때 무순리스트 L에 대한 부리스트 L1, L2는 각각 n/2개의 원소를 가진다.
2. 재귀단계에서는 L1과 L2를 재귀적으로 정렬한다.
3. 통치단계에서 정렬된 L1과 L2에 대해서 순서를 고려한 순서리스트로 합병한다.
위의 세단계를 그대로 수도코드로 작성해보자.
| Alg mergeSort(L) input list L with n elements output sorted list L 1. if (L.size() > 1) L1, L2 <- partion(L,n/2) ### 1번 분할 mergeSort(L1) mergeSort(L2) ### 2번 재귀 L <- merge(L1,L2) ### 3번 통치 2. return |
2번 재귀의 base case와 recursvie case를 고려해보자.
base case는 리스트의 사이즈가 1이하 일때까지이다. 즉 리스트가 단일 원소로 쪼개질때까지 무순 리스트L을 트리형태로 계속 분할 해나가는것이 되겠다.
그렇게 잘게 쪼개진 단일원소들을 3번 통치과정을 통해 순서리스트로 합치면 합병정렬이 구현된다.
그럼 3번 통치 merge 에 대한 알고리즘은 어떻게 될까?
| Alg merge(L1, L2) input sorted list L1, L2 with n/2 elements each output sorted list of L1 U L2 1. L <- empty list 2. while( !L1.isEmpty() & !L2.isEmpty()) if ( L1.get(1)<=L2.get(1)) L.addLast(L1.removeFirst()) else L.addLast(L2.removeFirst()) 3. while(!L1.isEmpty()) L.addLast(L1.removeFirst()) 4. while(!L2.isEmpty()) L.addLast(L2.removeFirst()) 5. return L |
직전학기에 수강한 자료구조에서 다룬 적이 있는 익숙한 수도코드이다.
두 리스트 중 하나의 원소가 끝날때까지, 리스트의 값들을 비교하면서 더 작은 값을 L에 넣고, 3,4번 과정에서
끝나지않은 나머지 리스트들까지 L에 넣어주는 알고리즘이다.

자동차가 2차선에서 1차선으로 진입하는 과정이라 생각하자.
결국 2차선 각각에 n/2 개의 자동차가 1차선으로 진입하게 되면, 1차선 도로에는 n개의 자동차가
주행하게 된다. 즉 합병하는데에 O(n) 시간이 소요된다.
합병정렬수행 예시1
합병정렬이 수행되면 처음에는 , 초기 호출을 통해 무순리스트 L이 L1,L2로 분할된다.

그리고 L1은 또 2개의 부리스트로 분할된다. 이때 이 과정은 재귀호출에 의해 이루어진다.
6,1,8,2의 리스트가 베이스케이스에 도달할때까지 3,5,7,4의 리스트는 대기

그리고 6,1,8,2 에 해당하는 리스트는 6,1// 8,2로 분할되는데
6,1 리스트가 다시 분할되고, 8,2 리스트는 위의 경우처럼 대기하게 된다.

6과 1로 분할되면서 base case에 도달했다. 따라서 6과 1은 분할이 끝나고, merge 가 수행된다.
즉 이전에 배운 1.분할 2.재귀 3.통치가 차례대로 수행되는 것.
merge 과정을 통해서 다음과 같은 그림이 된다.

merge 작업이 끝난 후에, 대기하고 있던 8,2 리스트에 대해서 다시 분할과 merge를 수행한다.
그럼 이렇게 된다
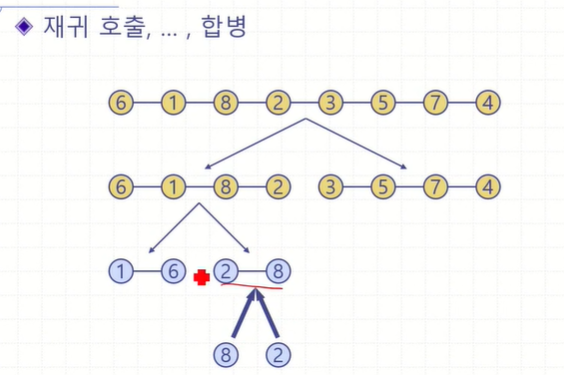
그리고 다시 올라가면서 1,6// 2,8 리스트가 merge 가 수행된다.

즉 처음에 L1 ==> 1,2,6,8 , L2 ==> 3,5,7,4 두개의 리스트로 나뉘어졌을때
L1에 대해서 모든 작업이 수행된 뒤에서야 L2가 수행되게 되는 것.
분할정복 알고리즘의 형태인것을 기억하고 이렇게 트리형태로 그림을 기억하는 것이 이해하기에 수월한 것 같다
따라서 마찬가지로 L2 (3,5,7,4) 리스트에 대해서도 위와 같은 작업을 수행하면 아래와 같다

그리고 마지막으로 1,2,6,8 + 3,4,5,7 을 merge 해주면 정렬된 리스트가 완성된다.

합병정렬수행 예시2
73 65 48 31 29 20 8 3
73 65 48 31 29 20 8 3
73 65 48 31 29 20 8 3
73 65 48 31 29 20 8 3 ##여기까지 분할
65 73 31 48 20 29 8 3
31 48 65 73 3 8 20 29
3 8 20 29 31 48 65 73
합병정렬 시간 분석
합병정렬 트리의 높이 h도 O(log n) 이다.
아까 합병정렬 실행 예시에서 분할작업을 할때
각 재귀호출에서 리스트를 절반으로 나누는 것을 보았었다. 따라서 O(log n)
깊이 i의 노드들에서 이루어지는 총 작업량은 O(n)이다.
이것은 실행예시에서 마지막에 n/2 크기의 L1,L2 두개의 리스트가 합병되는 과정을 생각해보면 당연하다.

다시 돌아와서 점화식으로 살펴보면
합병정렬의 경우 partition 수행에는 상수시간이 필요해서 고려x

T(n) = c (n<2)
T(n) = T(n/2) + T(n/2) + O(n) = 2*T(n/2) + O(n)
점화식을 풀면 T(n) = O(n*logn)
합병정렬 응용 : 배열에 대한 합병 정렬
배열에 대해서도 어렵지않게 이해할 수 있다.


'지난 학기들의 기록 > 알고리즘' 카테고리의 다른 글
| [강의노트] 사전ADT를 이용한 선형탐색과 이진탐색 - 1 (0) | 2021.10.05 |
|---|---|
| [강의노트] 합병정렬과 퀵정렬 - 2 (0) | 2021.09.30 |
| [강의노트] 힙과 힙정렬 - 3 (0) | 2021.09.25 |
| [강의노트] 힙과 힙정렬 - 2 (0) | 2021.09.07 |
| [실습] 상향식 힙 생성 (0) | 2021.09.07 |



댓글