| 삽입식 힙 생성 |
포스트에 게시된 것은 알고리즘 수업자료에 대한 기록입니다.
제가 작성한 소스코드에 대한 카피를 금지합니다.
| 힙은 이진트리로 구현된 우선순위 큐다. 여기서 이진트리를 배열을 이용해서 구현하면 순차트리 형태, ==> 순차힙 연결리스트를 이용하면 연결트리 형태로 구현할 수 있다. ==> 연결힙 우선순위 큐의 각 항목은 (키, 원소) 쌍이며 이진트리의 각 노드로 구현된다. 이진트리의 루트에 최소 키를 저장한 경우 최소힙, 반대로 최대 키를 저장한 경우 최대힙이라고 부른다. 힙 생성은 삽입식과 상향식의 두 가지 방식이 있다. 삽입식은 모든 키 들이 미리 주어진 경우, 또는 키들이 차례로 주어지는 경우 양쪽에 적용이 가능하다. 상향식은 모든 키 들이 미리 주어진 경우에만 적용 가능하다. 즉, 다시 말해서 동일 키들의 동일 순서로 구성된 초기 리스트라도 삽입식, 상향식 중 어느 방식을 적용하느냐에 따라 상이한 힙이 생성될 수 있다. |
프로그래밍 조건
이번에 구현해 볼 것은 삽입식 힙 생성이다. 문제에 몇가지 프로그래밍 조건이 있다.
1. 순차힙으로 구현한다. 즉 배열을 이용한 순차트리 형식으로 힙을 저장한다
2. 최대힙으로 구현한다.
3. 연산 효율을 위해 배열 인덱스 0 위치는 사용하지 않는다
4. 데이터구조를 단순화 하기 위해, 키만 저장한다
5. 키들은 중복이 없는 1 이상의 정수로 전제 ( 즉 중복 키 검사가 불필요하다)
6. O(1) 공간에서 수행한다. ( 즉 배열을 추가로 더 만들지 말라는 말)
7. 힙은 어느 시점에서라도 최대 항목 수가 100 미만이다.
문제 설명
키들은 한 개씩 차례로 삽입 명령과 함께 주어진다. 즉, 키가 입력될 때마다 즉시 힙에 삽입해야 한다. 만약 이렇게 하지 않고 문제 2에서 하는 것처럼 키들이 모두 입력되기를 기다려 한꺼번에 상향식으로 힙을 생성하면 대화식 프로그램의 인쇄(p) 또는 삭제(d) 명령의 수행이 어려워진다
대화식 프로그램에 주어지는 명령은 i, d, p, q 네 가지며 각 명령에 대해 다음과 같이 수행해야 한다.
- i <키> : <키>를 힙에 삽입하고 0을 인쇄.
- d : 힙에서 삭제(이때 루트에 저장된 키가 삭제되어야 한다)하여 반환된 키를 인쇄.
- p : 힙의 내용을 인쇄(이때 이진트리의 레벨순서로 항목들을 인쇄해야 한다).
- * 레벨순서란 이진트리의 레벨 0의 노드부터 다음 레벨 1, 2, 3, ...의 노드들을 차례로 방문한다. 같은 레벨의 노드들은 왼쪽에서 오른쪽으로 방문한다.
- q : 프로그램 종료
전역변수 초기화.
| #pragma warning(disable:4996) #include <stdio.h> #include <stdlib.h> int Heap[99]; int n; //힙의 크기, 현재 키의 개수 |
main( ).
◦ main() 함수
- 인자: 없음
- 반환값: 없음
- 내용: 반복적으로 i, d, p 명령에 따라 insertItem, removeMax, printHeap 함수를 각각 호출 수행, q 명령 입력 시 종료.
삽입식 힙 생성에 필요한 함수들을 하나씩 알아보자. 먼저 main 함수이다.
메인에서는 사용자로부터 i,d,p 명령을 입력받고, 각 명령에 맞는 함수를 호출한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
int main() {
/*
<command>
i : insert , p : print
d : delete , q : quit
*/
char command;
int key;
int root = 0;
while (1) {
scanf("%c", &command);
if (command == 'i') {
scanf("%d", &key);
//n위치에 key 삽입
insertItem(key);
printf("0\n");
}
else if (command == 'd') {
root = removeMax();
printf("%d\n", root);
}
else if (command == 'p') {
printHeap();
}
else if (command == 'q') {
break;
}
}
}
|
cs |
만약 command가 ' i ' 로 주어질경우에는 추가로 key를 입력받아야하는것에 주의하자.
또한 ' d ' 일때는 힙의 루트노드의 key를 반환받아야 한다.
insertItem(key).
- 인자: 정수 key
- 반환값: 없음
- 내용: n 위치에 key 삽입, upHeap(n) 호출 수행 후 n(총 키 개수)을 갱신 - 시간 성능: O(log n)
메인에서 입력받은 key 값을 현재 힙에 삽입한다.
insertItem 호출전에 힙의 크기가 n 이라면, 배열 인덱스 n+1 에 키 값을 삽입한다.
한번 수도코드를 살펴보자.
| Alg insertItem(k) input key k , node last output none 1. advanceLast() 2. z <- last 3. Set node z to k 4. expandExternal(z) 5. upHeap(z) 6. return |
쉽게 말해서, 새로운 키를 넣을 수 있게 노드를 확장하고, 망가진 힙순서를 복구하기위해 상향식 heapify를 수행하라는 뜻
|
1
2
3
4
5
6
7
8
9
10
|
void insertItem(key) {
//힙의 n+1 위치에 key 삽입
n = n + 1;
Heap[n] = key;
// 상향식 heapify
upHeap(n);
}
|
cs |
프로그래밍 조건에서 순차힙으로 구현하라는 요구가 있어서, 배열을 사용하다보니 상당히 단순해지게 된다.
현재 힙의 크기를 나타내는 전역변수 n을 1 증가시키고, 입력받은 key를 힙에 삽입한다.
그리고 상향식 heapify를 실행한다.
이 과정을 직관적으로 이해하기 위해, 실제 예시를 보자.
현재 9,7,6,5,4 의 key가 힙구조를 이루고 있다.

이때 insert 명령을 통해 8이 새로 삽입된다면?

힙순서가 망가졌다. root 노드의 오른쪽 sub tree가 힙구조를 이루고 있지 않은 것.
그래서 새로운 key가 삽입된 후에 upHeap 함수가 호출되는 것이다.

이때 상향식 힙이라고 부르는 이유는, 위 그림처럼 루트노드를 향해 올라가면서 힙순서를 구성하기때문
그렇다면 upHeap 함수를 알아보자.
upHeap(v).
- 인자: 배열 인덱스 i
- 반환값: 없음
- 내용: 힙 내 위치 i에 저장된 키를 크기에 맞는 위치로 상향 이동
- 시간 성능: O(log n)
즉 새로 삽입된 인덱스로 부터 루트노드까지 상향 이동하며, 최대 힙 크기에 맞는 인덱스로 설정되어야 함
수도 알고리즘을 살펴보자.
| Alg upHeap(v) input node v output none 1. if(isRoot(v)) return 2. if(key(v) >= key(parent(v)) return 3. swapElements(v,parent(v)) 4. upHeap(parent(v)) |
수도코드를 보면, 재귀 알고리즘인 것을 볼 수 있다.
재귀 알고리즘에서는 base case와 recursive case를 생각해야하는데,
먼저 base case는 현재 노드, 즉 순차힙에서는 인덱스가 root에 도달했을때이다. 즉 현재 삽입된 인덱스에서, 루트노드에 해당하는 인덱스로 갈때까지 상향이동하라는 것
recursive case는 현재 노드를 자식노드라 보았을때, 부모노드와 key값을 비교해서 더 크다면 swap 하는 것이다. 그 뒤에
현재 노드(자식노드)를 부모노드로 설정해 다시 반복한다.
어려운 재귀 알고리즘은 아니지만, 그래도 좀 더 직관적인 이해를 위해 다시 한번 예시를 통해 살펴보자

heap = [ 9,7,5,4,3,2,1 ] 에 해당하는 트리를 나타낸 것이다.
최대힙으로 힙순서가 구현된 모습이다. 여기서 10이 새로 삽입된다면 인덱스 8에 key값 10이 추가되어
다음과 같을 것이다.

이제 이 상황에서 재귀 알고리즘이 실행되는 과정을 살펴보자.

먼저 가장 하단의 subtree에서 자식노드인 10과 부모 노드인 4의 크기를 비교한다. 10이 더 크기 때문에 swap 된다

다음 수행은 아까 부모노드였던 인덱스 4 를 가지고 다시 호출하기때문에 한 칸 상향 이동한 sub tree에서 다시 같은 과정을 수행한다. 인덱스 4 (10) 과 인덱스 2 (7)을 비교한다. 인덱스 4 (10) 이 더 크기때문에 swap한다.

그 결과.

이전의 수행에서 부모노드였던 인덱스 2를 자식노드로 다시 호출하면서 아래의 sub tree에서 다시 한번 비교가 수행된다.

마찬가지로 10이 더 크기때문에 swap한다.

이제 현재 노드가 가리키는 인덱스가 1 이기때문에 upHeap(v)를 호출하게 되면 재귀 알고리즘의 base case인
isRoot(v)에 해당되어 재귀 알고리즘이 종료된다. 즉 상향식 heapify가 끝난것이다.
위의 과정에서 볼 수 있듯이, sub tree가 상향이동하기때문에 상향식 힙 생성이라고 부르는 것
그럼 이제 코드를 통해 구현해보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
void upHeap(int v) {
if (v == 1) { // isRoot ?
return;
}
int parent = v / 2;
if (Heap[v] <= Heap[parent]) {
return;
}
//swap
int temp = Heap[v];
Heap[v] = Heap[parent];
Heap[parent] = temp;
upHeap(parent);
}
|
cs |
위의 base case 에 해당하는 isRoot는 순차힙에서는 단순하게 루트 인덱스인지 체크만 해주면 되기때문에, 짧게 작성할 수 있다.
그 후에 parent는 현재 인덱스를 2로 나누어주면 된다. ( 초기 프로그래밍 조건에서 0번째 인덱스를 사용하지않아서 쉽게 구현되는 것)
현재 노드가 부모노드 보다 크다면 swap 하는 간단한 과정이다.
removeMax().
- 인자: 없음
- 반환값: 삭제된 키(정수) - 내용: downHeap 호출 수행 후 n(총 키 개수)을 갱신
- 시간 성능: O(log n)
힙구조에서 removeMax()는 루트노드를 삭제한 뒤 key값을 반환하는 것이다. (힙은 우선순위 큐이다)
| Alg removeMin() input node last output key 1. k ← key(root()) 2. w ← last 3. Set root to key(w) 4. retreatLast() 5. z ← rightChild(w) 6. reduceExternal(z) 7. downHeap(root()) 8. return k |
위의 수도코드를 간단히 말하자면, root 노드에 있는 key 값을 반환하고, 힙의 마지막 노드의 값을 root로 설정한 후에
현재 노드의 크기 n을 1 감소 시키는 것이다.
코드를 통해 이해하는 것이 더 빠르다.

마찬가지로 root 가 삭제되면서 힙순서 속성이 위배되었을 수 있기때문에, 다시 heapify를 수행해야하는데 이번에는
상향식 heapify가 아닌 하향식 heapify이다.
최대힙을 위해서 현재 root 노드에 가장 최솟값 key가 존재하기때문에 힙의 바닥까지 하향식 heapify를 수행해야하는것.
downHeap(v).
인자: 배열 인덱스 i
- 반환값: 없음
- 내용: 힙 내 위치 i에 저장된 키를 크기에 맞는 위치로 하향 이동
- 시간 성능: O(log n)
수도코드를 살펴보면 마찬가지로 재귀적인 알고리즘이다.
| Alg downHeap(v) input node v whose left and right subtrees are heaps output a heap with root v 1. if (isExternal(leftChild(v)) & isExternal(rightChild(v))) return 2. larger ← leftChild(v) {internal node} #자식노드 중 더 큰 값을 찾는 것. 3. if (isInternal(rightChild(v))) if (key(rightChild(v)) > key(larger)) larger ← rightChild(v) 4. if (key(v) >= key(larger)) # 현재노드의 자식노드 중 더 큰 값과 비교, 현재노드(부모노드)가 더 크다면 return return 5. swapElements(v, smaller) 6. downHeap(smaller) |
재귀 알고리즘이기때문에 base case를 살펴보면, 자식노드가 isExternal 이라면 재귀호출이 멈추게 된다.
즉 다시 말해서 현재 노드(부모노드)의 자식노드가 leaf 라면 재귀호출을 멈추게 되는 것.
이부분도 좀 더 쉽게 받아들이기 위해 예시를 살펴보자.

아까 만든 최대힙을 그대로 가져왔다. 여기서 removeMax()가 호출된다면? 아래와 같은 결과가 될 것이다.

힙순서 속성이 위배되었기때문에 하향식 heapify를 통해서 힙순서 속성을 복구한다.
두 개의 자식 노드, 인덱스2 (7) 과 인덱스3 (5) 중 더 큰 것은 leftChild 이다. 따라서 왼쪽 자식노드와 현재 노드를 비교한다. 왼쪽 자식 노드의 값이 더 크기때문에 swap 한다.
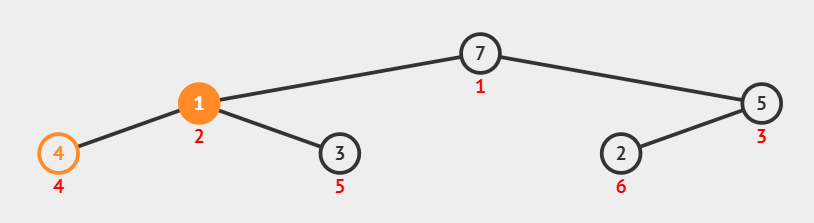
그리고 왼쪽 자식노드 인덱스2를 가지고 다시 downHeap(2)를 호출해서 같은 과정을 수행한다.
인덱스 4 (4) 가 더 크기때문에 또 swap한다.

처음 root 노드에 있던 1은 2번의 비교를 수행하고 나서 힙의 가장 하단에 위치하게 되었다.
이때 인덱스 4 에 해당하는 노드는 자식노드가 없으므로 재귀호출을 멈추는 base 케이스가 된다. 코드로 어떻게 구현하면 될까?
인덱스 4 가 부모노드라면 자식노드는 인덱스 8과 9가 된다. 따라서 힙의 총 크기를 나타내는 n이 8보다 작다면
현재 노드인 인덱스4의 자식노드가 없기때문에 재귀호출을 멈추면 된다.
코드를 살펴보자
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
void downHeap(int v) {
int left_child = 2 * v;
int right_child = 2 * v + 1;
// isleaf ?
// 현재노드의 자식노드가 없다면 return
if (left_child > n) {
return;
}
int larger = left_child;
//더 큰 자식을 찾고
if (Heap[right_child] > Heap[larger]) {
larger = right_child;
}
//자식과 부모노드를 비교해서, 자식이 크다면 교환
if (Heap[v] < Heap[larger]) {
int temp = Heap[v];
Heap[v] = Heap[larger];
Heap[larger] = temp;
}
//하향식 구조
downHeap(larger);
}
|
printHeap().

따로 설명할 부분이 없기때문에 코드로 생략.
소스코드
GitHub - nuguri-in-forest/sj_algorithm1: 2021 학년도 2학기 알고리즘 강의
2021 학년도 2학기 알고리즘 강의. Contribute to nuguri-in-forest/sj_algorithm1 development by creating an account on GitHub.
github.com
전체 코드는 위에서 참고 할 수 있습니다.
'지난 학기들의 기록 > 알고리즘' 카테고리의 다른 글
| [실습] 상향식 힙 생성 (0) | 2021.09.07 |
|---|---|
| [강의노트] 힙과 힙정렬 - 1 (0) | 2021.09.06 |
| [강의노트] 우선순위 큐와 힙 (0) | 2021.09.02 |
| [C 알고리즘] 힙 정렬 - Heap Sort Algorithm (0) | 2020.09.05 |
| [C 알고리즘] 병합 정렬 - Merge Sort Algorithm (0) | 2020.06.14 |




댓글