| 힙과 힙정렬 |
힙이란?
내부노드에 키를 저장하며 다음 두가지 속성을 만족하는 이진트리 ( 외부노드에는 키를 저장하지 않는다는 것 .)
| 힙순서(heap-order): 루트를 제외한 모든 내부노드 v에 대해, key(v) >= key(parent(v)) # 즉 자식노드가 부모노드보다 같거나 크다. ( 최소힙의 힙순서를 말함) 완전이진트리(complete binary tree): 힙의 높이를 h라 했을 때, i = 0 , ... , h - 1 에 대해 깊이 i인 노드가 2^i개 존재한다. # 즉 루트노드 부터 시작해서 트리의 하단으로 갈수록 2의 제곱만큼 개수가 늘어나는 것을 말함 깊이 h - 1 에서 내부노드들은 외부노드들의 왼쪽에 존재해야한다. # 왼쪽부터 채워지는 것을 말함 |

힙의 높이
| n개의 키를 저장한 힙의 높이는 O(log n) 이다. 증명:( 완전이진트리의 성질을 이용해서 증명할 수 있다.) 1. n개의 키를 저장한 힙의 높이를 h라고 하자. 2. 깊이 i = 0 , ... , h - 2에 2^i 개의 키, 그리고 깊이 h -1 에 적어도 한개의 키가 존재하므로, n >= 1 + 2 + 4 + . . . + 2^(h-2) +1 3. 따라서, n은 2^(h-1) 같거나 크고, h는 <= log(n)+1 보다 작다 |

힙과 우선순위 큐
힙을 사용하여 우선순위 큐를 구현 가능하다.
이전 포스트에서 이미 다룬 내용이므로 생략.

힙에 삽입

위의 그림을 보자. key 값이 1인 새로운 노드가 삽입된 모습이다. 새로운 노드가 삽입된 후에는, 내부노드로 만들어주어야하므로 왼쪽,오른쪽 자식 노드를 생성해준다. 그것이 expandExternal(z) 함수의 역할.
그 후에 heapify 를 통해 힙순서 속성을 복구하게 된다
Upheap.
새로운 노드가 삽입되고, 내부노드로 만들어준 뒤에 heapify를 수행하는데
상향식 heapify가 수행된다.
그림을 보자.

삽입노드로부터 상향 경로를 따라가며 키 k를 교환하여 힙순서 속성을 복구한다.
키 k가 루트에 ,또는 부모의 키가 k보다 작거나 같은 노드에 도달하면 정지한다.
Upheap의 수행 시간은 힙의 높이에 따른다. (상향 경로를 지나며 수행하므로)
힙의 높이는 O(log n) 이므로 upheap의 수행시간 또한 O(log n) 시간에 수행된다
힙 삽입 알고리즘.

이전 포스트에서 자세히 다룬 내용이므로 생략.
expandExternal(z) 알고리즘.
| Alg expandExternal(z) input external node z output none 1. l <- getnode() 2. r <- getnode() 3. l.left <- null 4. l.right <- null 5. l.parent <- z # 왼쪽 자식노드의 부모노드는 z 6. r.reft <- null 7. r.right <- null 8. r.parent <- z # 오른쪽 자식노드의 부모노드는 z 9. z.left <- l # z의 왼쪽 자식노드는 l 10. z.right <- r # z의 오른쪽 자식노드는 r 11. return |

어렵지 않은 내용이므로 설명은 필요없을듯 하다.
힙으로부터 삭제.

삭제 알고리즘 세단계를 살펴보자
1. 루트키를 마지막 노드키로 대체
2. reduceExternal 즉 아까 노드를 내부노드로 만든 과정의 역과정이라 생각하면 된다
3. 힙순서 속성 복구( 이번에는 하향식 heapify가 수행된다 그 과정은 다음 downHeap에서 알아보자)
downHeap.
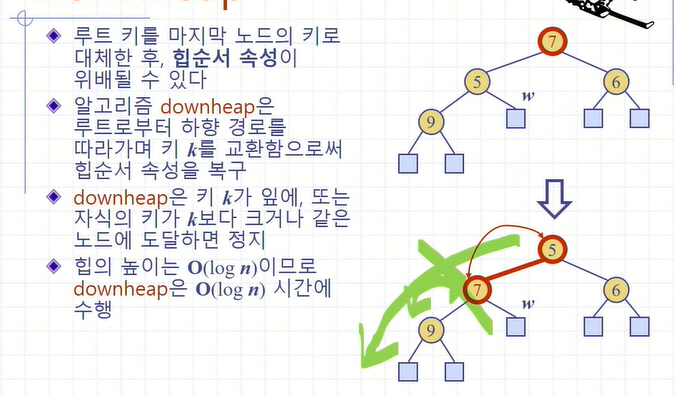

이 과정에 대한 자세한 설명은 이전 포스팅에서 다루었으므로 생략.
reduceExternal(z) 알고리즘.
expandExternal 과 비교했을때 조금 생각할 것이 있기때문에 먼저 그림을 통해 알고리즘 진행 과정을 이해해보자

w노드가 삭제되어야하고 그의 자식노드들은 외부노드가 되어야한다.
즉 다시 말해서 w노드가 삭제될 때 w노드의 오른쪽 자식노드도 함께 사라지므로 두개의 노드가 삭제되는 것이다.
왼쪽 자식은 승진되는 것이라 이해하자
그 결과 w노드는 zs와 z라는 자식노드를 가진 내부노드 였는데, 왼쪽 자식노드 zs만 남아서 외부노드가 되었다.
이 과정을 통해 내부노드가 외부노드로 축소되는 것이다.
| Alg reduceExternal(z) input external node z output the node replacing the parent node of the removed node z 1. w <- z.parent 2. zs <- sibling(z) 3. if(isRoot(w)) root <- zs zs.parent <- null else g <- w.parent zs.parent <- g if ( w = g.left) g.left <- zs else g.right <- zs 4. putnode(z) 5. putnode(w) 6. return zs ## putnode는 free 를 의미한다. 4~6 부분도 주의해서 보자 |
수도코드를 살펴보기전에 결과를 먼저 기억하자.
위 수도코드의 목표는 w와 z노드를 삭제하는 것이다.

먼저 w를 z의 부모노드로 설정한다.
z노드를 zs 노드에 치환한다.
만약 w노드가 루트노드라면, zs노드가 루트노드가 되고. zs의 부모노드는 없다
w노드가 내부노드라면, g가 w노드의 부모가 되고, zs의 부모노드는 g가 된다. 이 과정에서 w가 삭제된다.
그리고 g와 zs를 연결하기전에, zs가 w의 왼쪽자식인지 오른쪽 자식인지 체크한 뒤에
g와 zs를 연결한다
그리고 삭제된 z와 w노드는 메모리를 반납한다
마지막 노드 갱신 알고리즘.
앞서 다룬 삽입과 삭제 알고리즘을 다시 한번 살펴보자

수도코드의 1번에 advanceLast( ).
즉 마지막 노드의 전진을 의미하는 알고리즘이 보인다.

삭제 알고리즘에서는 반대로, retreatLast( ) 마지막 노드의 후퇴를 의미하는 알고리즘이 나온다.
마지막 노드를 갱신하는 두 알고리즘은 어떻게 작동하는 것인지 알아보자.

먼저 advanceLast 알고리즘이다.
위와 같은 그림에서 현재 화살표를 통해 last node 를 지정하고 있다.
이때 만약 새로운 노드가 삽입된다면, insertion node 가 지정하고 있는 위치에 노드가 삽입될 것이다.
삽입 알고리즘에서 1번 과정이 advanceLast 이기때문에, 노드를 삽입하기전에 마지막 노드를 갱신해야한다.
눈으로 보았을때는 단순히 last node를 오른쪽으로 한 칸 옮기는 단순한 과정인 것으로 보이지만 실제 코드로는 단순하지않다. 답은 빨간 점선이 나타내고 있다.
시계 방향으로 동그랗게 돌면서 last node에서 insertion node가지 순회하면서 삽입 노드를 찾게된다.
다시 말하면 advanceLast 알고리즘의 핵심은 last node에서 insertion node로 이동하는 과정을 작성하면 된다.
| 1. 현재 노드가 오른쪽 자식인 동안, 부모 노드로 이동한다. 2. 현재 노드가 왼쪽 자식이라면, 형제 노드로 이동한다. 3. 현재 노드가 내부노드인동안, 왼쪽 자식으로 이동한다. 위의 3가지 알고리즘을 순서대로 진행하면 성공적으로 last node 에서 insertion node 로 이동할 수 있다. |
1 -> 2-> 3의 과정을
그림으로 표시하면 다음과 같다.

코드로 작성해보면 1번 알고리즘에 해당하는 while 문 하나
2번 왼쪽 자식 노드에서 오른쪽 자식노드로 이동하는 코드
3번 알고리즘에 해당하는 while 문 하나 로 작성할 수 있을 것이다.
다음은 후퇴를 의미하는 retreatLast 알고리즘이다. 위의 1 -> 2 -> 3 과정을 단순히 반대로 진행하면 된다.
따라서 자세한 설명은 생략하겠다.
'지난 학기들의 기록 > 알고리즘' 카테고리의 다른 글
| [강의노트] 힙과 힙정렬 - 2 (0) | 2021.09.07 |
|---|---|
| [실습] 상향식 힙 생성 (0) | 2021.09.07 |
| [실습] 삽입식 힙 생성 (0) | 2021.09.05 |
| [강의노트] 우선순위 큐와 힙 (0) | 2021.09.02 |
| [C 알고리즘] 힙 정렬 - Heap Sort Algorithm (0) | 2020.09.05 |




댓글