| 우선순위 큐 |
우선순위 큐가 무엇인가?
우선순위가 가장 높은 데이터를 먼저 삭제하는 자료구조.
데이터를 우선순위에 따라 처리하고 싶을 때 사용함.
| 스택 : 가장 나중에 삽입된 데이터를 추출 큐 : 가장 먼저 삽입된 데이터를 추출 우선순위 큐 : 가장 우선순위가 높은 데이터를 추출 |
우선순위 큐를 구현하는 방법
1. 단순히 리스트를 이용하여 구현.
2. 힙을 이용하여 구현
힙(Heap)의 특징
힙은 완전 이진 트리 자료구조의 일종이다.
여기서 완전 이진 트리란 힙의 높이를 h라 했을때 i=0 , . . ., h-1 에 대해 깊이 i인 노드가 2^i개 존재 하고
깊이 h-1 에서 내부노드(자식이 있는 노드)들은 외부노드(자식이 없는 노드)들의 왼쪽에 존재하는 트리
쉽게 말하면 루트 노드부터 시작해서 자식노드가 형성될 때 왼쪽 자식노드 -> 오른쪽 자식노드 순서대로 데이터가 차례대로 삽입되는 것
| 힙에서는 항상 루트 노드를 제거한다. 최소 힙 : + 루트 노드가 가장 작은 값을 가지게 된다. + 따라서 값이 작은 데이터가 우선적으로 제거된다. 최대 힙 : + 루트 노드가 가장 큰 값을 가진다. + 따라서 값이 큰 데이터가 우선적으로 제거된다. |
최소 힙 구성 함수: Min-heapify()

위에서 다루었듯이, 힙 구조에는 조건이 필요하다. 최소 힙 성질을 만족하기 위해 트리의 노드들을 이동시키는 것을 heapify 라고 한다. 예시처럼 최소 힙 성질을 만족시키기 위해서 트리의 노드 위치를 변경시키는 것은 min-heapify 라고 한다.
이렇게 heapify 함수를 통해서, 트리에 새로운 원소가 삽입되었을때 O(logN)의 시간복잡도를 가지고 힙 성질을 유지하도록 할 수 있다.
우선순위 큐 ADT

우선순위 큐 ADT의 메소드

우선순위 큐를 이용한 정렬

| 1. P <- empty priority queue # 비어있는 우리 2. while( !L.isEmpty()) # 울타리속이 비어있지 않는동안 e <- L.removeFirst() # 울타리로부터 맨 앞에 있는것부터 삭제한다. P.insertItem(e) # 우리에 울타리로부터 삭제된 elem을 삽입한다. 3. while(!P.isEmpty()) # 우리가 비어있지 않는동안 e <- P.removeMin() # 우리에서 가장 키가 작은 동물(data)를 삭제한다. L.addLast(e) # 키가 가장 작은 동물 (data)를 울타리의 마지막에 삽입한다. 4. return |
무순리스트로 구현한 우선순위 큐 - 선택정렬

먼저 무순리스트로 구현한, 우선순위 큐를 알아보자.
이 알고리즘을 selection-sort 즉 , 선택정렬이라고 부른다.

먼저 n번 insertItem 작업을 사용해서, 동물들을 우선순위 큐에 삽입한다. O(n) 시간 소요

그리고 n회 우선순위 큐 로부터 가장 키가 작은 동물들을 찾아서 삭제한다.
이 작업에선 n + (n - 1) + (n - 2) + . . . + 2 + 1 의 시간이 걸린다.
즉 Total Big O 시간은 O(n^2) 이다.
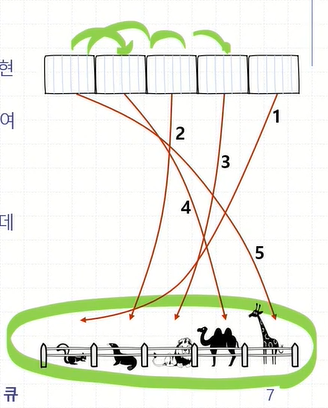
즉 최종적으로, 키 순서로 정렬되어 울타리에 저장되게 된다.
순서리스트로 구현한 우선순위 큐 - 삽입정렬



각 동물이 우선순위 큐에 삽입 되는 과정은, 적절한 자리를 찾고(비교) 삽입되는 것이다
따라서 실행시간이
0 + 1 + 2 + ... + (n-2) + (n-1) + n 의 시간이 필요하다.
마지막으로 울타리로 다시 옮기는 과정은 removeMin인데 이미 정렬되어있으므로
n회번 동안 상수시간(remove)작업을 해주면 되므로 O(n)이다.
따라서 Total은 O(n^2) 시간.
제자리 정렬
제자리(in-place) 정렬
"제자리에서 할 수 있나"?
선택정렬과, 삽입정렬은 모두 O(n) 공간을 차지하는 외부의 우선순위 큐를 사용하여 리스트를 정렬한다.
근데 만약, 원래 리스트 자체를 위한 공간 이외에 O(1)의 공간만을 사용한다면 이를 제자리(in-place)에서 수행한다고 말한다.
일반적으로, 어떤 정렬 알고리즘이 정렬 대상 개체를 위해 필요한 메모리 외에 오직 상수 메모리만을 사용한다면
해당 정렬 알고리즘이 제자리 에서 수행한다고 말한다.
+ 여기서 상수메모리란 ?
입력값 n 의 크기에 비례하는 공간이 아닌, 상수개의 변수가 차지하는 메모리 공간을 말함
예를 들어, int 형 변수 x,y,z . . 등을 선언해서 사용해도 상수개의 변수를 선언해서 사용하는 것이기때문에
여전히 제자리에서 정렬을 수행했다고 말할 수 있음.
위에서 다룬, 선택정렬과 삽입정렬은 O(n)에 해당하는 외부 공간을 사용해서 리스트를 정렬했기때문에 제자리 정렬이 아니다. 그렇다면 제자리 정렬방식으로 선택정렬과 삽입정렬을 구현할 수 있을까?
제자리 선택 정렬 . O(n^2)
선택정렬을 제자리에서 수행하도록 구현할 수 있다.
| 조건. + 리스트의 앞부분을 정렬 상태로 유지한다 + 리스트를 변경하는 대신 swapElements 를 사용한다 |
별로 어려운 개념이 아니다. 이전에 새로운 공간으로 이동하는 대신, 앞부분을 정렬된 상태로 유지한다.
다음 수행에서 이미 정렬된 공간은 배제하고 수행을 반복한다.
| Alg inPlaceSelectionSort(A) input array A of n keys output sorted array A 1. for pass <- 0 to n-2 minLoc <- pass for j <- (pass+1) to n - 1 if ( A[j] < A[minLoc]) minLoc <- j A[pass] <-> A[minLoc] 2. return #리스트의 앞부분부터 최솟값을 삽입한다. #다음 수행에서는, 이미 정렬된 인덱스 뒤에서 부터 최솟값을 다시 찾는다. |
제자리 삽입 정렬 . O(n^2)
삽입정렬을 제자리에서 수행하도록 구현할 수 있다.
| 조건. + 리스트의 앞부분을 정렬 상태로 유지한다 + 리스트를 변경하는 대신 swapElements 를 사용한다 |
삽입정렬은 매 원소가 삽입될 때 자신의 자리를 찾는 것이다. 선택정렬과 비교했을 때 살짝 더 어렵다고 느낄 수 있으나
수도코드를 통해 이해하면 매우 쉽다.
| Alg inPlaceInsertionSort(A) input array A of n keys output sorted array A 1. for pass <- 1 to n - 1 save <- A[pass] j <- pass -1 while (( j>=0 ) & (A[j] > save )) A[j+1] <- A[j] j <- j -1 A[j+1] <- save 2. return |
각 원소가 삽입될때마다, 현재 인덱스에서 처음 인덱스까지 바로 옆의 원소와 비교하면서 이동한다.
그리고 인덱스가 0이 된다면 반복을 멈추고 다음 수행을 시행한다.
선택 정렬 vs . 삽입 정렬

알아둬야할 것.
- 전체적으로 O(n^2) 시간 알고리즘이다.
- O(1)의 공간이 소요된다.
- 구현이 단순하다.
- O(n^2)의 시간이 걸리기때문에 작은 n에 대해서는 유용할 수 있다.
초기 리스트가 완전히 또는 거의 정렬된 경우
삽입정렬의 내부 반복문에 while 조건에 위배되므로, 내부 반복문이 O(1) 시간 소요된다.
따라서 전체적인 시간이 O(n)이 된다.
선택정렬은 매 반복마다 크기 비교를 위한 반복을 시행해야하므로 여전히 O(n)이다.
★ 따라서 이 경우에는 삽입 정렬이 더 빠르다. ★
성능 요약

'지난 학기들의 기록 > 알고리즘' 카테고리의 다른 글
| [강의노트] 힙과 힙정렬 - 1 (0) | 2021.09.06 |
|---|---|
| [실습] 삽입식 힙 생성 (0) | 2021.09.05 |
| [C 알고리즘] 힙 정렬 - Heap Sort Algorithm (0) | 2020.09.05 |
| [C 알고리즘] 병합 정렬 - Merge Sort Algorithm (0) | 2020.06.14 |
| [C 알고리즘] 퀵 정렬 - Quick Sort Algorithm (0) | 2020.05.12 |




댓글