| 이코테 - DFS & BFS |
본 게시물은 이것이 코딩테스트다(저자 나동빈님)의 책을 구매하고 공부하는 과정에서 남기는 정보공유의 목적보다
개인적인 기록에 가까운 포스팅입니다.
작년 여름에 구매한 책을 봉인해뒀다가 다시 꺼내들었다. 어떻게 하다보니 알고리즘까지 다 수강한 상태에서 다시 공부하게됐는데 좀 수월한면이 있는거같다.
이번 챕터는 DFS 와 BFS 이다.
개념은 다 알고 있기때문에 가볍게 복습하는 느낌으로 작성할 예정이다.
스택과 큐 구현
스택구현은 따로 라이브러리 호출없이 append 함수와 pop 함수를 활용해서 구현한다.

큐는 deque 라이브러리를 사용하고, append와 popleft함수를 활용한다

DFS
https://man-25-1.tistory.com/184
[강의노트] 그래프 순회 - 1 (DFS와 싸이클찾기)
그래프 순회 - 1 그래프를 구현하는 문제에 대해서 지난 시간에 해결해보았다. 이번에 배울것은 그래프 순회이다. 깊이우선탐색과 너비우선탐색은 내가 알고리즘을 공부하기전에도 매우 자주
man-25-1.tistory.com
위 게시글에서 DFS를 재귀호출로 구현하는 것을 공부했었다.
DFS는 그래프의 시작 정점에서 인접노드를 타고타고 계속해서 깊숙하게 들어가면서 탐색하는 것이었다.


스택의 최상단노드를 기준으로 더 이상 방문하지않은 인접노드가 없을 때, pop을 한다.
소스코드 구현은 재귀호출로 구현하는데, 어차피 원리는 같다. 재귀호출이 스택프레임에 쌓였다가 수거되는 과정을
위에서 노드가 스택에 쌓이는 과정이라고 이해하면 된다.

BFS
https://man-25-1.tistory.com/186
[강의노트] 그래프 순회 -2 (BFS)
그래푸 순회 - 2(BFS) 지난 포스트에서는 DFS에 다루어보았고, 이번에 배울것은 BFS 너비우선탐색이다. 마찬가지로 그래프 순회 기법이다. BFS - 너비우선탐색 너비우선탐색에서 가장 핵심적인 단어
man-25-1.tistory.com
깊이 파고파고 들어가는 dfs와 다르게 bfs는 같은 level 노드(형제노드)들을 다 탐색하고 다음 level로 내려가는 탐색 방법이다.

언뜻보면 비슷해보이지만 이번에는 스택이 아닌 큐 를 이용해서 탐색한다. dfs와 동작과정에서의 차이를 확연하게 알아보기 위해 이번에는 순서대로 한번 살펴보자.
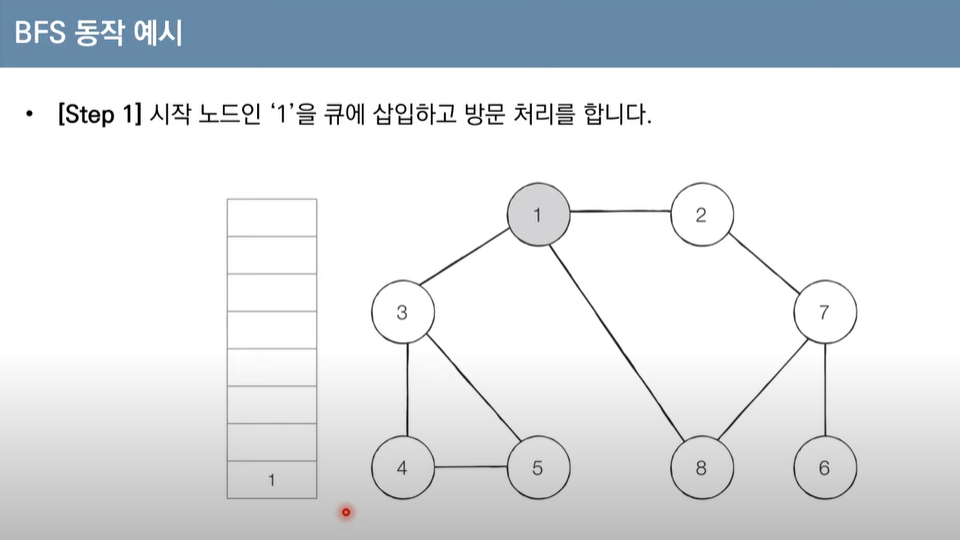


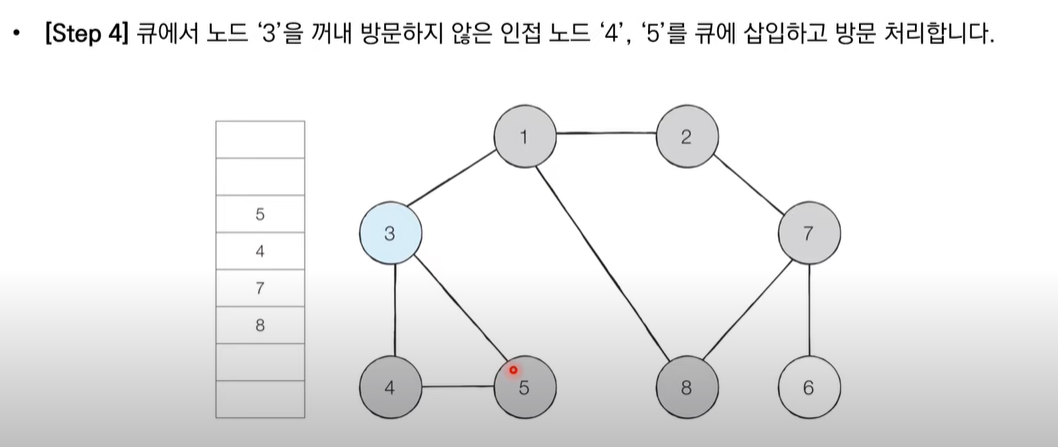
깊이 우선 탐색과는 다르게 같은 level의 인접노드(즉 탐색 시작노드부터의 거리가 가까운 노드)를 먼저 탐색하는 모습을 볼 수 있다.


소스코드를 보면 dfs와 다르게 재귀를 사용하지않은 것을 볼 수 있는데
아까 재귀호출로 함수가 스택프레임에 쌓이는과정은 노드가 스택에 쌓이는 과정과 유사했기때문에 재귀를 쓴 것이고
bfs는 큐를 사용해서 구현하는 것이기때문에 재귀로 구현하지않는다.

이제 실습문제를 해결해볼 차례이다.
실습1 음료수 얼려먹기 : 그래프의 연결요소 개수 찾기

일단 dfs,bfs를 활용하는 문제니까 당연하게도 dfs를 활용해야한다.
dfs를 활용하기위해 그래프형태로 모델링해서 보면 조금 더 생각하기가 쉬워진다.

즉 그래프에서 연결요소가 몇개인지 찾아내는 것이 문제에서 요구하는 사항이다.
위의 예시를 가지고 문제해결 과정을 생각해보자
2차원 리스트로 그래프를 표현해서, 각 정점에 대해서 dfs를 수행한다면 첫번째 연결요소는 0,0의 정점에서의 dfs 호출로 모든 인접 정점을 방문하게 된다.
그리고 얼음 판은 다음과 같이 바뀌게 된다.
1 1 1
1 1 0
1 0 1
그럼 0,1 0,2 1,0 1,1 의 정점은 다 방문한 상태이므로, 1,2의 정점에서 dfs 호출이 되고
그 결과는
1 1 1
1 1 1
1 0 1 이 된다.
마찬가지로 반복하면 총 3개의 정점에서 dfs를 수행하면 모든 얼음판의 구멍이 뚫려있는 정점을 방문하게 되는 것이다.
한 정점에서 깊이우선탐색을 하듯 너비우선탐색을 하든 각 연결정점들을 완전탐색하는 것은 같기때문에 bfs를 써도 상관없다. 그래프의 연결요소 개수를 확인하기 위해서는 dfs(or bfs)를 호출한 시작정점이 방문하지않은 정점인지만
확인해주면 된다는 것을 이해하는 것이 중요하다.
|
def dfs(x,y):
#x,y는 좌표
if x<=-1 or x>=N or y<=-1 or y>=M:
return False
if graph[x][y] == 0 :#방문하지않은 노드이면
graph[x][y] = 1 # visited
#상하좌우에서 dfs 재귀호출
dfs(x-1,y)
dfs(x,y-1)
dfs(x+1,y)
dfs(x,y+1)
return True
return False
N,M = map(int,input().split())
graph = []
for i in range(N):
graph.append(list(map(int,input())))
result = 0
for i in range(N):
for j in range(M):
if dfs(i,j)== True:
result += 1
print(result)
|
실습2: 미로 탈출

최단거리를 구하는 문제이다. 시작지점에서 출구까지의 최단거리를 묻고 있다.

위와 같은 5x6 직사각형 형태의 미로에서 출발점에서 최단경로로 도착지까지 가는 방법은 출발지와 도착지를 포함해서 총 10칸을 이동해야한다.
문제를 해결하는 아이디어는
시작 정점에서 이동가능한 인접 정점으로 이동할때마다 최단거리를 계속해서 갱신하는 것이다.
예를 들어 아래와 같은 3x3 의 정사각형에서 1을 따라서 미로를 탈출할때의 최단거리를 생각해보자.
파란색으로 표시된 시작정점에서 출발하면 오른쪽으로 갈 수 있다.

그렇게되면 최단거리를 2로 갱신하는 것이다.

마찬가지로 아래로 내려가면 3, 4, 5 .. 이렇게 계속해서 갱신해가면서 시작정점에서 각 정점까지의 최단거리를 계산하면서 노드를 탐색한다.

즉 BFS를 호출하면 인접한 모든 정점을 탐색하게 되는데, 각 정점에 대해 도달할 때 최단거리를 갱신해주는 것이 문제풀이아이디어라고 할 수 있다.
| from collections import deque def bfs(x,y): queue = deque() queue.append((x,y)) while queue: x,y = queue.popleft() for i in range(4): nx = x + dx[i] ny = y + dy[i] if nx <0 or nx >=N or ny <0 or ny>=M: continue if graph[nx][ny] == 0: continue if graph[nx][ny] == 1: graph[nx][ny] = graph[x][y] + 1 queue.append((nx,ny)) return graph[N-1][M-1] N,M = map(int, input().split()) graph = [] for i in range(N): graph.append(list(map(int,input()))) dx = [-1,1,0,0] dy = [0, 0, -1,1] print(bfs(0,0)) |
실제로 모든 정점에 대해 최단거리를 출력해보면 아래와 같다.

최단거리를 갱신하는 과정에서 이전 정점의 인덱스 x,y 와 인접 정점의 인덱스 nx, ny가 필요하기때문에
재귀호출을 통해 동작하는 dfs로 풀이하기에는 적절하지 않은 것 같다.
즉 여기까지 정리하면
dfs, bfs 를 통해 구할 수 있는 가장 기본적인 값 3가지인
1. 호출 횟수를 통해 연결요소 개수 구하기
2. 각 연결요소를 이루는 정점의 수 구하기
3. 최단거리 구하기
이렇게 구하는 방법을 배워보았다.
'개인 공부 > 이코테' 카테고리의 다른 글
| 이코테 - 다이나믹 프로그래밍(dp) (0) | 2022.09.16 |
|---|---|
| 이코테 - 구현: 시뮬레이션과 완전 탐색 (0) | 2021.08.18 |
| 이코테 - 그리디 알고리즘 (0) | 2021.08.11 |



댓글