| 그리디 알고리즘이란? |
본 게시물은 이것이 코딩테스트다(저자 나동빈님)의 책을 구매하고 공부하는 과정에서 남기는 기록에 가까운 포스팅입니다. 따라서 이 게시물에 대한 저작권은 책의 저자인 나동빈님에게 있음을 알립니다.
그리디 알고리즘은 현재 상황에서 지금 당장 좋은 것만 고르는 방법을 의미한다.
+ 일반적인 그리디 알고리즘은 문제를 풀기 위한 최소한의 아이디어를 떠올릴 수 있어야함.
+ 그리디 해법은 그 정당성 분석이 중요하다.
이 과정에서 단순히 가장 좋아 보이는 것을 반복적으로 선택해도 최적의 해를 구할 수 있는지 검토합니다.

위와 같은 문제가 주어질 때, 어떤 아이디어를 생각할 수 있을까?
첫번째 가장 단순하게 떠오르는 아이디어는, 각 노드에서 다른 노드로 이동해야하는 선택상황마다 가장 큰 값만 고르는 것이다.

그렇다면 위와 같이 5 -> 10 -> 4 의 경로로 이동하는 해를 얻게되고, 총 합은 19이다.
따라서 5->7->9 ( 총합 21)보다 크기가 작으므로, 최적의 해가 아니다.
위에서 사용한 아이디어는 , 각 선택 상황에서 단순히 가장 큰 값에 해당하는 노드로 경로를 설정한 그리디 알고리즘이다. 예시에서도 알 수 있듯이, 그리디 알고리즘은 일반적인 상황에서 최적의 해를 보장할 수 없을때가 많다.
하지만 코딩 테스트에서의 대부분의 그리디 문제는 탐욕법으로 얻은 해가 최적의 해가 되는 상황에서, 이를 추론할 수 있어야 풀리도록 문제가 출제된다.
대표적인 문제 예시를 통해 그리디 알고리즘을 알아보자.

이 문제에 대한 가장 직관적인 아이디어는 다음과 같다.
가장 큰 화폐 단위인 500원부터 돈을 거슬러준다.
즉 예를 들어 1260원을 거슬러 주어야한다고 생각해보자.
500원을 최대한 거슬러주면 2개이다. 1260 - 1000 =260
100원을 최대한 거슬러주면 2개이다. 260 - 200 = 60
50원을 최대한 거슬러주면 1개이다. 60 - 50 = 1
10원을 최대한 거슬러주면 1개이다. 10 - 10 = 0
따라서 총 동전의 개수는 6개이다.
| 화폐 단위 | 500 | 100 | 50 | 10 |
| 손님이 받은 개수 | 2 | 2 | 1 |
위의 거스름돈 문제에서 정당성을 분석해보자.
가장 큰 화폐단위부터 돈을 거슬러준다는 아이디어가 최적의 해를 보장하는 이유가 무엇일까?
그것은 가지고 있는 동전 중에서 큰 단위가 항상 작은 단위의 배수이므로, 작은 단위의 동전들을 종합해서 다른 해가 나올 수 없기 때문이다.
즉, 다시 말해서 거스름돈 문제에서 가장 큰 화폐단위부터 돈을 거슬러주는 아이디어는 가지고 있는 동전이 큰 단위가 작은 단위의 배수인 경우에만 정당성이 보장된다는 뜻이다.
예를 들어 800원을 거슬러 주어야하는데, 화폐 단위가 500원, 400원 ,100원 인 경우를 생각해보자.
위에서 적용한 그리디 알고리즘을 통해 해를 구하면 500원 1개 100원 3개 즉 구한 해는 4개이다.
하지만 최적의 해는 400원 동전 2개이다.
이렇듯 그리디 알고리즘 문제에서는 문제 풀이를 위한 최소한의 아이디어를 떠올린 다음
이것이 이 문제에서 정당한 아이디어인지 검토할 수 있는 능력이 필요하다.

위에서 문제 풀이에 사용한 알고리즘을 파이썬으로 구현한 내용이다.
알고리즘에 대한 시간 복잡도를 분석해보자.
| 화폐의 종류가 K라고 할 때, 소스코드의 시간 복잡도는 O(K) 이다. 이 알고리즘의 시간복잡도는 거슬러주어야 하는 금액 n 과는 무관하며, 동전의 총 종류의 수에만 영향을 받는다. |
이제 예시문제를 통해 학습해보자.
<문제> N이 1이 될 때까지.
어떠한 수 N이 1이 될 때까지 다음의 두 과정 중 하나를 반복적으로 선택해서 수행하려고 한다.
단 두번째 연산은 N이 K로 나누어 떨어질 때만 선택할 수 있다.
1. N에서 1을 뺍니다.
2. N을 K로 나눕니다
예를 들어 N이 17이고, K가 4라고 가정해보자.
이때 1번 과정을 수행하면 N이 16이 되고, 2번 과정을 두번 진행하면 N이 1이 된다.
결과적으로 답은 3번이 될 것이다.
N과 K가 주어졌을 때, N이 1이 될 때까지 1,2번의 과정을 수행해야하는 횟수의 최솟값을 출력하라.

직관적으로 아이디어를 생각해보자.
먼저 2번과정은 N이 K로 나누어 떨어질 때만 선택할 수 있다는 조건이 붙는다. 다시 말해서, 우선적으로
N이 K로 나누어떨어지는지 검사하고, 나누어떨어진다면 2번과정을 수행하고, 나누어 떨어지지않는다면 1번 과정을 수행한다.
아래는 내가 작성해 본 코드이다.

최적의 해를 구하기 위해서는 N이 1이 되는 과정에서 가능한 최대 횟수의 나누기를 보장해야한다. K가 2이상이기때문에 빼기 과정 보다 더 빠르게 N을 1로 만들 수 있기때문이다.
아래는 책에서 제시한 예시답안이다.

코드를 보았을 때, 직관적으로 와닿지 않아서 예시를 통해 이해해보려고 했다.
N이 17 , K가 4일때 처음 수행을 고려해보자.
target 의 값은 17을 4로 나눈 몫의 값인 4에 4를 곱해서 16이 된다.
즉 target 변수의 의미는 k로 나눌 수 있는 n과 가장 가까운 수를 말한다. 즉 17은 4로 나눌 수 없지만
17과 가장 가까운 4의 배수는 16이 된다.
그렇다면 result의 값은 무슨 뜻일까?.
result는 N을 K로 나누기 위해, N에 얼마만큼의 값을 빼야하는지를 말한다.
즉 result의 값은 1번과정을 진행한 횟수를 의미할 것이다.
이제 빼는 횟수를 구해주었으므로, n을 다시 나누어떨어지는 수인 target으로 업데이트한다.
n이 k보다 작을때, 반복문을 탈출하고 그게 아니라면, result에 1을 더한후에(나눗셈에 더한 카운팅)
n을 k로 나눈다.
큰 틀에서 위의 과정이 한번의 수행이라 볼 수 있고, 요약하자면 나누어떨어지는 수가 될 때까지 빼고
나누는 것 이라고 요약할 수 있겠다.
시간복잡도를 두고 분석해보면, 내가 작성한 알고리즘은 빼기 과정에서 1씩 뺄때와 나누기를 할때마다 반복문이 돌아가야하지만 답안에 제시된 알고리즘은 필요한 횟수 만큼의 뺄셈 + 나눗셈 한번의 과정이 반복 한번에 일어나기때문에
훨씬 효율적인 알고리즘이라고 볼 수 있다.
<문제> 곱하기 혹은 더하기

문제를 읽자마자 느낀 것은, 그리디 알고리즘을 만들어주는 조건이 존재한다는 것이다. 이번 문제도 특정 조건이 없었다면 상당히 복잡한 문제로 느껴질 수 있었지만, 첫번째 문단의 마지막 줄에, 일반적인 계산 방식과는 다르게 모든 연산은 왼쪽부터 순서대로 이루어진다고 가정하라 되어있다. 이 부분이 문제를 단순하게 만들어주면서, 그리디 알고리즘으로 최적해를 구할 수 있도록 만들어주는게 아닐까 생각했다.
곱하기와 더하기 연산자를 통해 가장 큰 숫자를 만들어야한다. 당연히 최대한 많이 곱하면 되지 않을까? 라는 생각이 일차원적으로 들었다. 하지만 예시로 주어진 문자열인 02984를 보았을 때 예외 사항이 떠올랐다.
0 의 경우에는 숫자뒤에 더하기 연산을 사용하고, 나머지의 숫자 뒤에는 곱셈을 해주면 될 것 같다
라고 생각하고 문제를 해결하려고 했으나 한가지의 예외가 더 있었다.
1의 경우에도 곱하기보다 더하기가 더 큰 값이기때문에 ( 1을 곱하면 자기자신) 1이하인 숫자에 대해서는 덧셈을
그게 아닌경우에는 곱셈을 진행해주면 된다

어려운 부분이 없고, 나 또한 같은 방식으로 작성했으므로 내 코드는 생략 !
<문제> 모험가 길드

예를 들어
| 모험가 5명의 사람이 존재하고 각 인원의 공포도는 2 3 1 2 2 라고 설정하자. 가장 높은 공포도를 가진 2번째 모험가는 적어도 3명이상의 그룹에 속해야 하므로 한 개의 그룹에는 최소 3명의 인원이 필요하다. 따라서 첫번째 그룹은 3명을 고정. 남은 2명의 인원을 각각 한명씩 배치해서 그룹을 3개 만드는 방법을 고려해보았을 때, 공포도가 1인 모험가가 한명뿐이므로 불가능하다. 따라서 남은 2명의 인원이 들어갈 두번째 그룹이 생성된다. 따라서 첫번째 그룹에는 (2,2,3) 두번째 그룹에는 (1,2) 등 과 같이 구성될 수 있고(그룹의 개수는 고정, 모험가 구성은 바뀔 수 있음) 정답은 2개의 그룹이다. 또한 몇 명의 모험가는 마을에 그대로 남아 있어도 되기 때문에, 모든 모험가를 특정한 그룹에 넣을 필요는 없다. |
처음에 이 문제에 대한 알고리즘을 생각할 때 잘 떠오르지가 않았다.

최대한 많은 그룹을 형성하려면 모험가들의 공포도는 낮을수록 좋다.
예를 들어서 5명의 모험가 모두 공포도가 1이라고 생각해보자.
각 그룹에 한명씩 5개의 그룹을 형성할 수 있다. 따라서 공포도가 낮은 모험가를 우선적으로 고려해야한다는 것을 알 수 있다.
그렇기때문에 우선적으로 모험가들을 공포도에 따라 오름차순으로 정렬한다.
그리고, 앞에서 부터 공포도를 하나씩 확인하여 현재 그룹에 포함된 모험가의 수가 현재 조회중인 모험가의 공포도보다
크거나 같다면 그룹으로 설정하면 된다.
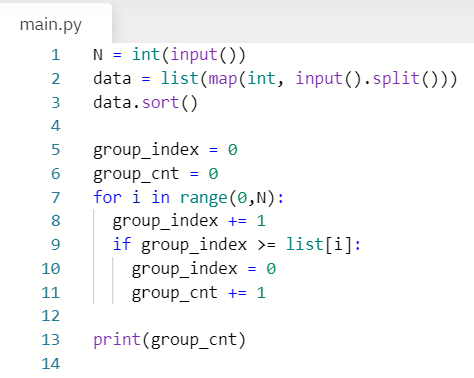
내가 작성한 알고리즘이 답안과 거의 유사하기때문에 뒤는 생략하겠다.
'개인 공부 > 이코테' 카테고리의 다른 글
| 이코테 - 다이나믹 프로그래밍(dp) (0) | 2022.09.16 |
|---|---|
| 이코테 - DFS & BFS (0) | 2022.04.09 |
| 이코테 - 구현: 시뮬레이션과 완전 탐색 (0) | 2021.08.18 |



댓글