| 시뮬레이션과 완전 탐색 |
본 게시물은 이것이 코딩테스트다(저자 나동빈님)의 책을 구매하고 공부하는 과정에서 남기는 기록에 가까운 포스팅입니다.
이번 포스팅에서는 구현 알고리즘 중 시뮬레이션과 완전 탐색에 대해서 다루게 될 것이다.
구현이란 쉽게 말해서 머릿속에 있는 알고리즘을 소스코드로 바꾸는 과정이다.

내가 C프로그래밍을 수강했었을때 풀이한 여러가지 유형의 문제들도 다 구현문제라고 생각하면 된다.
흔히 알고리즘 대회에서 말하는 구현 유형의 문제란 풀이를 떠올리는 것은 쉽지만 소스코드로 작성하는 것이 어려운 문제를 지칭한다.
| 1. 알고리즘은 간단한데 코드가 지나칠 만큼 길어지는 문제 2. 실수 연산을 다루고, 특정 소수점 자리까지 출력해야하는 문제 3. 문자열을 특정한 기준에 따라서 끊어 처리해야하는 문제 4. 적절한 라이브러리를 찾아서 사용해야 하는 문제 |

행렬에서 방향벡터 개념을 사용해서 문제를 풀이하는 유형이 자주 등장한다
<문제> 상하좌우


5x 5 의 행렬 공간에서
R R R U D D 만큼 움직이면
1,1 에서 출발하여
-> (1,2) -> (1,3) -> (1,4) -> (1,4) -> (2,4) -> (3,4) 가 되는 것
중간에 1,4에서 UP은 위로 이동할 공간이 없으므로 무시된다.
이렇듯 구현 유형의 문제는 아주 단순하게 풀이를 떠올릴 수 있지만 소스코드로 작성하는 것에 난이도가 있는 문제이다.
이런 유형의 문제는 자주 풀어봤기때문에 소스코드는 쉽게 작성했다.

<문제> 시각

아이디어를 떠올리는 것은 간단하다. 문제 그대로 00시 00분 00초 부터 N시 59분 59초까지 초 단위의 각 시각에 3이 포함되어있는지 구현하면 되기때문이다.
만약 c를 사용했더라면 일의자리와 십의자리 각각을 확인해야해서 조금 번거로웠겠지만, 파이썬을 이용하면 간단하게 구현가능하다.
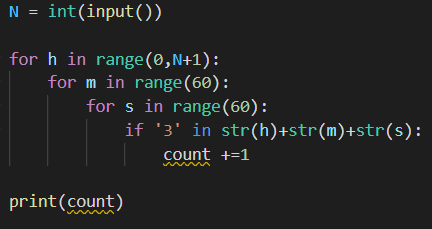
이렇게 파이썬에서는 정수를 문자열처리해서 포함관계를 간단하게 알 수 있기때문에 꼭 기억해두자.
<문제> 왕실의 나이트

8x8 좌표평면에서 다음과 같은 방법으로 말을 움직일 수 있다.
1. 수직 2칸 이동과 수평 1칸 이동 (4가지 경우)
2. 수평 2칸 이동과 수직 1칸 이동 (4가지 경우)
문제는 현재 위치에서 1,2번 방법의 각 이동 경우의 수에 대해 체스 판을 벗어나는지를 확인하는 것이다.
총 이동 경우의수는 8가지밖에 안돼서 별 다른 아이디어를 떠올릴필요없이 각각을 그냥 검사하면 된다고 생각이 들었다.
| array = [[0 for col in range(8)] for row in range(8)] x,y = map(int,input().split()) count = 0 # 1. 수직 위 2칸 이동 +수평 좌 1칸 point_y = y-2 point_x = x-1 if point_x>=0 and point_y>=0: count += 1 # 2. 수직 위 2칸 이동 +수평 우 1칸 point_y = y-2 point_x = x+1 if point_x<=7 and point_y>=0: count += 1 # 3. 수직 아래 2칸 이동 +수평 좌 1칸 point_y = y+2 point_x = x-1 if point_x>=0 and point_y<=7: count += 1 # 4. 수직 아래 2칸 이동 +수평 우 1칸 point_y = y+2 point_x = x+1 if point_x<=7 and point_y<=7: count += 1 # 1. 수직 위 1칸 이동 +수평 좌 2칸 point_y = y-1 point_x = x-2 if point_x>=0 and point_y>=0: count += 1 # 2. 수직 위 1칸 이동 +수평 우 2칸 point_y = y-1 point_x = x+2 if point_x<=7 and point_y>=0: count += 1 # 3. 수직 아래 1칸 이동 +수평 좌 2칸 point_y = y+1 point_x = x-2 if point_x>=0 and point_y<=7: count += 1 # 4. 수직 아래 1칸 이동 +수평 우 2칸 point_y = y+1 point_x = x+2 if point_x<=7 and point_y<=7: count += 1 print(count) |
이러고 해설코드를 봤는데 좀 부끄러웠다
그냥 방향벡터 8가지를 정의해서 for문을 이용하면 되는거였다.. 어차피 조건도 0<=x,y<=7 이 공통사항이라 중복해서 적을 필요도 없으니까

다음번에 비슷한 문제가 나오면 방향벡터를 정의해서 풀이에 활용하자.
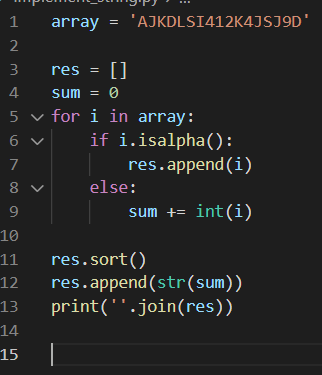
<문제> 문자열 재정렬

https://man-25-1.tistory.com/56
[C실습] 문자열 유형 분석 1 - 문자열에서 숫자 분리하기
문자열 유형 분석 1 - 문자열에서 숫자(정수) 추출하기 저번 포인터 과제에 이어서 문자열 과제에서도 연속해서 등장한 문제로, 문자열에서 숫자를 빼내는 연습을 해보겠습니다. 문자열에서 숫
man-25-1.tistory.com
이런 유형은 이미 많이 다뤄봤기때문에.. 특히 파이썬은 제공해주는 메소드가 너무 많아서 아주 간단하게 구현가능하다
'개인 공부 > 이코테' 카테고리의 다른 글
| 이코테 - 다이나믹 프로그래밍(dp) (0) | 2022.09.16 |
|---|---|
| 이코테 - DFS & BFS (0) | 2022.04.09 |
| 이코테 - 그리디 알고리즘 (0) | 2021.08.11 |



댓글