| 단일연결리스트를 이용한 합병 정렬 |
https://man-25-1.tistory.com/163
[강의노트] 합병정렬과 퀵정렬 - 1
합병정렬과 퀵정렬 합병정렬과 퀵정렬에 대한 강의 노트입니다. 분할통치법 합병정렬에 대해 알아보기전에 먼저 분할통치법의 개념에 대해 알아보자. 쉽게 말해서 큰 문제를 작은 문제로 나
man-25-1.tistory.com
지난 시간에 다루었던 합병정렬을 실제로 구현해보려고 한다.
간단하게 개념을 복습해보면, 합병정렬은 분할통치법으로 3단계 구성으로 구현된다.
분할 -> 재귀 -> 통치(합병) 단계로 이루어지는데 이때 합병정렬에서 가장 중요한 단계는 merge 알고리즘이다.
퀵 정렬에서는 분할 알고리즘이 핵심이고, 합병정렬은 통치 알고리즘이 핵심이었던 것을 기억하자.
| Alg mergeSort(L) input list L with n elements output sorted list L 1. if (L.size() > 1) L1, L2 <- partion(L,n/2) ### 1번 분할 mergeSort(L1) mergeSort(L2) ### 2번 재귀 L <- merge(L1,L2) ### 3번 통치 2. return |
| Alg merge(L1, L2) input sorted list L1, L2 with n/2 elements each output sorted list of L1 U L2 1. L <- empty list 2. while( !L1.isEmpty() & !L2.isEmpty()) if ( L1.get(1)<=L2.get(1)) L.addLast(L1.removeFirst()) else L.addLast(L2.removeFirst()) 3. while(!L1.isEmpty()) L.addLast(L1.removeFirst()) 4. while(!L2.isEmpty()) L.addLast(L2.removeFirst()) 5. return L |
merge sort에 대한 수도코드 알고리즘이다. 대략적인 설명은 이미 다 공부했었기때문에 생략하고 이번에 집중적으로 다루어 볼 것은 merge 즉 통치에 대한 알고리즘이다.
merge 알고리즘 수도코드는 다음과 같다.
사실 수도코드는 이해하는것이 어렵지 않다. 빈 리스트에다가 L1 , L2 의 원소들을 비교해가면서 차례대로 리스트에 삽입하는 과정이기때문에 직관적인 이해가 가능하다.
다시 말해서 배열의 경우라면 인덱스를 이용해서 위의 수도코드를 그대로 참고하면, 매우 간단하게 구현할 수 있다.
https://man-25-1.tistory.com/35?category=938895
[C 알고리즘] 병합 정렬 - Merge Sort Algorithm
정렬 알고리즘에서 퀵 정렬을 배운뒤 병합정렬 알고리즘을 접해보았습니다. 나동빈님의 블로그와 유튜브 강의를 통해 개념을 학습했는데 설명이 잘되어있어서 참고용으로 기록을 하기 위해 포
man-25-1.tistory.com
하지만 단일연결리스트로 구현해야한다면?. 즉 L1, L2 말고 추가로 메모리를 사용할 수 없다면 어떻게 할 수 있을까?
단일연결리스트로 구현한 merge sort
1. merge 알고리즘 이해하기
반복해서 말했듯이 merge sort의 핵심은 3번 통치과정이다.
그렇기때문에 아래의 단순한 문제를 통해 단일연결리스트에서의 merge 알고리즘을 먼저 파악해보자.
| 각 3개의 원소를 오름차순으로 입력해서 연결리스트 L1, L2을 생성합니다. 그리고 두 리스트 L1, L2를 merge 알고리즘을 통해 병합해서 최종적으로 정렬된 리스트를 출력하세요. 입력 예시) 1 3 5 ==> L1 2 4 6 ==> L2 출력 예시) 1 2 3 4 5 6 |
바로 코드를 통해 알아보자.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
|
#pragma warning(disable:4996)
#include <stdio.h>
#include <stdlib.h>
typedef struct node {
struct node* next;
int data;
}NODE;
NODE* makenode(int data) {
//make a new_node
NODE* new = malloc(sizeof(NODE));
new->data = data;
new->next = NULL;
return new;
}
NODE* merge(NODE* L1, NODE* L2) {
NODE* res = NULL;
//2차선 도로의 차들이 1차선으로 합쳐지는 원리
//base case
if (L1 == NULL) return L2;
else if (L2 == NULL) return L1;
//recursive case
if (L1->data < L2->data) {
res = L1;
res->next = merge(L1->next, L2);
}
else {
res = L2;
res->next = merge(L1, L2->next);
}
return res;
}
int main() {
NODE* L1=(NODE*)malloc(sizeof(NODE));
L1->next = NULL;
NODE* L2=(NODE*)malloc(sizeof(NODE));
L2->next = NULL;
int data;
NODE *cur = L1;
//L1 리스트 생성
for (int i = 0; i < 3; i++) {
scanf("%d", &data);
cur->next = makenode(data);
cur = cur->next;
}
cur = L2;
for (int i = 0; i < 3; i++) {
scanf("%d", &data);
cur->next = makenode(data);
cur = cur->next;
}
NODE* res;
res = merge(L1->next, L2->next);
printf("\n=======합병 결과=====\n");
for (int i = 0; i < 6; i++) {
printf("%d ", res->data);
res = res->next;
}
}
|
cs |
코드의 한 부분씩 뜯어서 살펴보자. 먼저 메인메소드에서 리스트를 생성하는 코드이다

L1과 L2는 각 리스트의 헤더로 사용했다. L1, L2에는 data를 두지않고 그 다음 포인터부터 data를 입력하도록 구현했다.
만약 예시와 같이 입력한다면 다음과 같이 두개의 연결 리스트가 생성된다.

입력을 받은 후에 각각 헤더의 next를 인자로 보내주면서 merge 메소드를 호출한다.

여기가 핵심인 merge 알고리즘인데 재귀형식으로 구현했기때문에 좀 어려울 수 있다.
결국 목적은 L1, L2 의 data를 비교해서 더 작은 원소를 리스트에 추가해 정렬된 연결리스트를 만드는 것이 목적이라는 것을 다시 한번 되뇌이자.

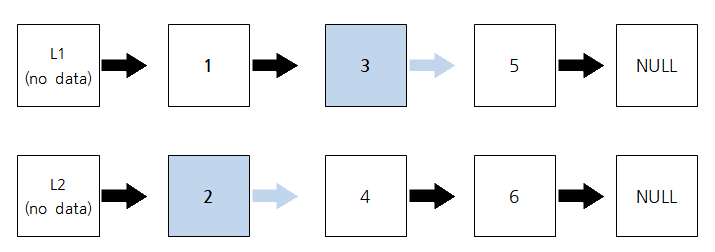
메소드가 호출된 뒤 처음 상태를 생각해보자. 메인에서 헤더의 next를 인자로 주었기때문에 초기 상황은 다음과 같다.
파란색으로 칠해진 부분이 현재 merge 메소드에서 L1, L2 포인터가 가리키고 있는 부분이라 생각하면 된다.


그리고 코드를 살펴보면 재귀호출의 방식을 사용한다. base case에 도달할때까지 한번 쫒아가보자.
처음 수행에서 L1->data = 1 이고 L2->data = 2 이기때문에 L1의 값이 더 작다.
따라서 다음 과정이 수행된다.
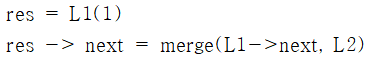
이때 L1 뒤에 괄호안의 숫자는 위의 코드가 수행될 때 L1의 포인터가 가리킨 data 값을 말한다.
그리고 L1->next를 통해 다시 한번 merge 가 호출되었다.

이번에는 L1-> data는 3이고, L2-> data는 2이다. 따라서 다음의 과정이 수행된다.


이제 설명은 생략하고 그림으로 계속 진행해보겠다.
L1.data < L2. data 이므로



L2.data < L1. data 이므로


L1. data < L2.data 이므로


이때 merge 호출에서의 L1 은 null 포인터를 가리키게되므로 base case에 도달한다.
base case를 다시 살펴보면

L1 이 지금 NULL에 도달했으므로, L2를 반환해야한다. 현재 호출에서 L2는 L2(6) -> next = NULL 이다.
base case에 도달했으므로 이제 거꾸로 올라가보자

빨간색으로 칠해진 부분부터 함수가 반환되며 이제 거꾸로 올라가는 것이다. 코드가 실행되면 res 포인터가 가리키는 연결리스트는 다음과 같이 생성된다.

그리고 다시 재귀과정을 거슬러 올라가며 위의 과정을 반복.

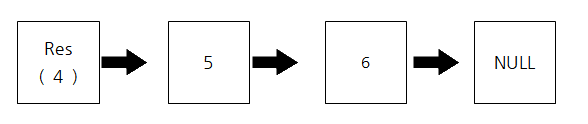
어차피 같은 과정이기때문에 다 생략하면 최종적으로 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> NULL 의 연결리스트가 만들어진다.
사실 이렇게 나열하고보니 큰 의미가 있나싶지만 재귀과정을 한번 쯤 실제로 확인해두면 좀 더 이해하기 수월할 때가 많았기때문에 도움이 된 것 같다.
2. 단일연결리스트를 이용한 merge sort 구현하기
실제 실습 문제를 해결해보자.
| - mergeSort(L) 함수: 단일연결리스트 L의 원소들을 합병 정렬하여 정렬된 결과를 오름차순으로 정렬 - merge(L1, L2) 함수: mergeSort에 호출되어 두 개의 정렬된 단일연결리스트 L1과 L2를 합병한 하나의 단일연결리스트를 반환. L1과 L2 합병을 위해 O(1) 공간만 추가 사용 가능. - partition(L, k) 함수: 단일연결리스트 L과 양의 정수 k를 전달받아 L을 크기가 k이고 |L| – k 인 두 개의 부리스트 L1과 L2로 분할하여 (L1, L2)를 반환. 여기서 |L|은 L의 크기. 분할 시에도 주어진 L 공간 외에 O(1) 공간만 추가 사용 가능 |
위의 3개 함수를 활용해서,
n개의 원소를 가지는 단일연결리스트 L을 생성하고, 최종적으로 정렬된 리스트를 출력하라.

각자 해결해보세용 !
'지난 학기들의 기록 > 알고리즘' 카테고리의 다른 글
| [강의노트] 해시 테이블 - 1 (0) | 2021.10.25 |
|---|---|
| [강의노트] 사전ADT를 이용한 선형탐색과 이진탐색 - 3 (0) | 2021.10.13 |
| [강의노트] 사전ADT를 이용한 선형탐색과 이진탐색 - 2 (0) | 2021.10.05 |
| [강의노트] 사전ADT를 이용한 선형탐색과 이진탐색 - 1 (0) | 2021.10.05 |
| [강의노트] 합병정렬과 퀵정렬 - 2 (0) | 2021.09.30 |




댓글