| 사전ADT를 이용한 선형탐색과 이진탐색 - 3 |
사전ADT 3번째 강의노트로 아래의 두 게시글에 이어지는 내용입니다.
사전ADT를 이용한 선형탐색과 이진탐색 - 1
[강의노트] 사전ADT를 이용한 선형탐색과 이진탐색 - 1
사전ADT를 이용한 선형탐색과 이진탐색 - 1 먼저 이전시간까지 다룬 정렬알고리즘들을 복습할 겸 정리해보고, 새로 배울 내용인 사전 ADT를 공부해보자. 비교정렬 알고리즘의 비교 정렬의 안정성
man-25-1.tistory.com
사전ADT를 이용한 선형탐색과 이진탐색 - 2
[강의노트] 사전ADT를 이용한 선형탐색과 이진탐색 - 2
사전ADT를 이용한 선형탐색과 이진탐색 - 2 https://man-25-1.tistory.com/172 [강의노트] 사전ADT를 이용한 선형탐색과 이진탐색 - 1 사전ADT를 이용한 선형탐색과 이진탐색 - 1 먼저 이전시간까지 다룬 정렬
man-25-1.tistory.com
지난 포스팅에서는 BST( binary search tree) 에 대해서 다뤘다. 간단히 복습하면 이진탐색트리는
key(leftchild) < key(parent) < key(rightchild) 를 만족하는 트리이다. 즉 트리를 중위순회로 탐색하면 키가 증가하는 순서로 방문하게 되는 것
이런 BST는 편항트리인경우 탐색 성능이 나빠지는 단점이 존재했었다.
AVL트리

정의에서도 알 수 있듯이, 편향트리가 되는 경우를 막아서 높이밸런스가 맞춰진 이진탐색트리형태이다.
AVL의 핵심은 다음과 같다.
좌, 우 자식노드의 높이 차이가 1을 넘지않는다
"""
여기서 트리의 높이가 나오는데, 간단하게 복습하면
트리의 높이는 현재 노드를 기준으로 외부노드까지 가는 경로의 최대 길이이고
깊이는 현재 노드를 기준으로 루트노드로 가는 최단 길이이다.
"""
따라서 AVL 트리는 탐색이나 삽입, 삭제 과정에서 이진탐색트리보다 높은 성능을 보여준다. ( O(logn) 보장 )
한가지 주의해야 할 것은 위의 예시에서 볼 수 있듯이 각 노드에 높이정보가 표시 되어있는데
코드로 구현할 때 각 내부노드에 높이 정보도 같이 저장되어야한다는 것
AVL트리의 갱신작업
AVL트리에서 삽입과 삭제 작업은 이진탐색트리에서의 삽입 및 삭제 작업과 유사하다. ( 베이스가 이진탐색트리이므로)
하지만 삽입이나 삭제 작업의 결과 AVL 트리의 높이균형속성이 파괴될 수 있다. 따라서 삽입과 삭제 작업이 이뤄진 후에는 혹시 생겼을지도 모르는 높이 불균형을 찾아서 수리해야한다.
불균형을 찾는 것은 각 노드의 균형검사를 통해, 그리고 불균형을 수리하는 것은 개조라 불리는 작업을 통해 수행한다.
정리하면, AVL 트리에서의 삽입과 삭제는 BST 트리와 유사하다. 단 높이균형속성이 파괴되지 않았을 때만
높이균형속성의 회복은
1. 균형검사(balance check)
2. 개조(restructure)
두 단계를 통해 이뤄진다.
AVL트리에서 삽입

그림에서는 AVL 트리에 새로운 원소 54를 삽입하는 것을 보여주고 있다. 그 결과 높이 불균형이 발생했다.
삽입된 노드(54)를 기준으로 부모노드를 따라 올라가다보면, 노드(78)에 도달했을때 왼쪽 자식노드(50)의 높이는 3이고, 오른쪽자식노드(88)의 높이는 1이다.
여기서 불균형이 발생했으므로, 개조를 해주어야한다.
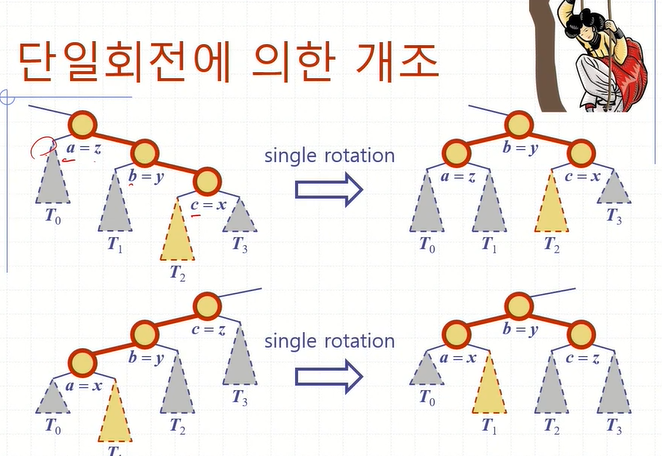
결론을 먼저 말하면 개조후의 트리의 모습은 아래 그림과 같다.



2. z의 높은 자식을 y라 하자.
: 삽입한 쪽에서 높이 불균형이 일어날 수 밖에 없으므로, y는 w의 조상이 된다.
3. y의 높은 자식을 x라 하자.
: 마찬가지로 삽입한 쪽에서 높이 불균형이 일어날 수 밖에 없으므로, x는 노드 w의 조상이 되거나 일치한다.




AVL트리에서 삭제





'지난 학기들의 기록 > 알고리즘' 카테고리의 다른 글
| [강의노트] 해시 테이블 - 2 (0) | 2021.10.29 |
|---|---|
| [강의노트] 해시 테이블 - 1 (0) | 2021.10.25 |
| [실습] 단일연결리스트를 이용한 합병정렬(merge sort) (0) | 2021.10.08 |
| [강의노트] 사전ADT를 이용한 선형탐색과 이진탐색 - 2 (0) | 2021.10.05 |
| [강의노트] 사전ADT를 이용한 선형탐색과 이진탐색 - 1 (0) | 2021.10.05 |




댓글