| 방향 그래프 - 2 |
https://man-25-1.tistory.com/187
[강의노트] 방향 그래프 - 1
방향 그래프 - 1 지금까지 무방향 그래프의 구현과 수정, 그리고 순회알고리즘 DFS와 BFS에 대해서 다루어보았다. 이번에 배울 것은 간선에 방향성이 존재하는 방향그래프이다. 방향그래프 방향그
man-25-1.tistory.com
방향 그래프의 여러 개념들에 대해 배워보았고 이제는 구현방법에 대해 알아볼 차례이다.
동적프로그래밍
그전에 지난 포스팅에서 다루었던 동적 프로그래밍의 개념에 대해 한번 짚고 가면
동적프로그래밍은 언뜻 보기에 많은 시간이 소요될 것 같은 문제에 주로 적용된다.
적용 조건은
1. 부문제들이 단순해야한다 - 부문제들이 j, k, l, m 과 같은 몇 개의 변수로 정의 되어야한다
2. 전체의 최적치가 최적의 부문제들에 의해 정의될 수 있어야한다
3. 부문제들이 독립적이지않고, 상호 겹쳐야한다. 따라서 해가 "상향식"으로 구축되어야한다
예시는 피보나치 수열에서 n번째 수찾기, 그래프의 이행적폐쇄 계산하기 등이 있다.
분할통치법과 비교하면 다음과 같다.

방향 비싸이클 그래프(DAG, directed acyclic graph)
방향싸이클이 존재하지 않는 방향 그래프
대표적인 예시는 교과목 간의 선수 관계가 있다. DAG를 이해할 때 적절한 예시가 되기때문에 꼭 기억해두자.

위의 그래프의 경우는 가로를 축으로 했을때, 좌우 방향중 우측으로만 이동가능하다. 즉 되돌아 올 수 없다는 뜻이다.
이때문에 방향싸이클이 존재하지 않는 것이다.
DAG와 위상정렬
위의 특성때문에 DAG 의 경우 위상순서를 가지게 되는데, 위상순서가 무엇일까?
위상순서는 모든 i < j인 간선 (v_i, v_j)에 대해 정점들을 번호로 나열한 것이다. 즉 번호가 작은 정점에서 큰 정점으로 이동하는 간선만
존재하는 것이다. 그림을 살펴보면 쉽게 이해할 수 있다.

즉 방향그래프가 DAG면 위상순서를 가지는 것은 당연하다. 위의 그래프는 아까 말했다싶이 방향싸이클이 없기때문에
좌 -> 우 순서대로 정점들에 번호를 주면 위상순서를 만들 수 있다.
이러한 위상순서는 예를 들어 작업스케줄링 방향 그래프에서 작업들의 우선순서가 필요할때 활용할 수 있다.

방향그래프가 DAG면 위상순서를 가지며 위상순서를 가지는 그래프 G는 DAG이다.
위의 그래프에서 위상순서는
A B C D E
B A C D E
가 가능하다.
이때, DAG로 부터 위와 같은 위상순서를 얻어내는 절차를 위상 정렬이라고 한다.

그럼 위에서 나와있는 위상 정렬 알고리즘에 대해서 알아보자
정점의 진입차수를 이용하는 위상 정렬

수도코드를 바로 이해하려고 들기보다 예시를 통해 수행 과정을 한번 살펴보는게 좋다.
아래의 그래프에서 위상순서를 구해보자.

먼저 위상순서의 처음 시작은 정점 A 또는 D이다. 위상순서에서 정점 A와 D가 시작 정점이 될 수 있는 이유는 진입간선이 존재하지 않기때문이다. 즉 다시 말해서 위상순서의 시작 정점을 구할때는 진입간선이 존재하지 않는 정점을 채택한다.
예시에서는 A를 시작 정점으로 설정해서 위상순서를 구하고 있다. 즉 초기상태에서 진입간선이 존재하지 않는 정점 A,D 중 A를 시작 정점으로 설정해서 위상순서는 A->D가 된다.
그 다음 순서를 고려해보자.
이미 순서가 정해진 정점 A와 D에서 출발하는 간선을 제외했을때 진입간선이 존재하지 않는 정점은 E가 된다.
따라서 위상순서는 A -> D-> E가 된다.
정점 A,D,E 에서 출발하는 간선을 제외하면 진입간선이 존재하지않는 정점은 B가 된다.
위상순서는 A -> D -> E-> B가 된다.

같은 방식으로 진행하면
최종 위상순서는 A -> D-> E-> B -> F-> C 가 된다.
여기서 한가지 생각해볼 것은, 만약 위상순서를 구하는 과정에서 더 이상 진입간선이 존재하지 않는 정점이 없다면 무슨 의미일까?
바로 싸이클을 만난 것을 의미한다.

위의 그래프에서 첫번째 페이즈 1,2에 대한 위상순서를 구하고 정점 1,2에서 출발하는 간선을 지웠을 때
진입간선이 존재하지않는 정점이 없다. 즉 싸이클을 만난 것이다.
이렇게 수행과정을 살펴보았을 때, 위 알고리즘을 구현한다고 생각하면 가장 핵심적인 것은 진입간선이 존재하지 않는 정점을 판단하는 것이다. 이 판단 알고리즘을 어떻게 구현할 수 있을까 생각해보자.
1. 먼저 그래프에 존재하는 정점들의 모든 진입간선의 수를 미리 다 구해두고, 진입간선이 없는 정점을 큐에 저장한다.

2. 큐에서 하나씩 뽑아온다. 아래 예시에서는 A를 가져왔고, A에서 나가는 간선의 종점에 있는 B와 E 정점에 진입간선의 수를 하나씩 줄인다. (B와 E의 진입간선 수를 2개에서 1개로 줄임)
3. 큐에서 D를 뽑아와서 D에서 나가는 간선의 종점에 있는 E의 진입간선의 수를 1에서 0으로 줄인다. 이때 E의 진입간선의 수가 0이 되었으므로 큐에 삽입한다.
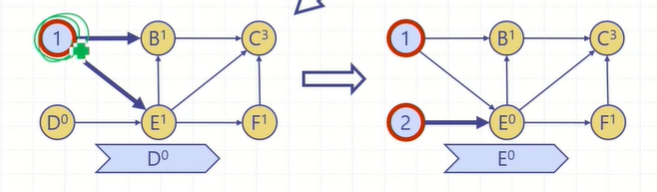
이제 수도코드를 다시 살펴보자.

수도코드의 번호 순대로 설명하면
1. 큐를 선언
2. 그래프 정점들의 진입차수 계산
3~4. 큐에서 진입간선이 0인 정점을 뽑아서, 그 정점에서 나가는 간선의 종점에 위치한 정점의 진입차수를 1 줄인다. 만약 진입차수가 0이 되는 정점이 있다면 큐에 삽입한다.
큐가 비어있을때까지 반복한다.
5. 만약 위의 과정이 끝났는데도 번호가 안 붙어있는 정점이 있다면 싸이클이 존재한다는 것
DFS를 특화 위상정렬
이번에는 DFS를 특화한 위상정렬에 대해서 알아보자.

마찬가지로 수도코드를 살펴보기전에, 예시를 통해 DFS를 특화한 위상정렬의 수행과정을 먼저 살펴보자.

A를 시작 정점으로 잡고, DFS순회를 통해 방향 간선을 따라 이동하면 C에 도착한다. C에서는 더 이상 이동할 수 있는
진출간선이 존재하지 않으므로 갇히게 된다. 즉 이 말은 위상순서에서 마지막인 것을 의미하기때문에 C의 위상순서는 6이 된다.
마찬가지로, C를 제외하고 살펴보면 B 또한 갇히게된다. 따라서 B의 위상순서는 5가 된다.

B에서 다시 되돌아가서, A노드에서 방문하지않은 다른 방향간선을 통해 이동하면 F에 도달하게된다. 마찬가지로 F는 갇혀있기때문에 위상순서 4가 되고, F가 제거되면 E가 갇히므로 위상순서 3이 된다. 그리고 E가 제거되었으므로 A로 돌아가면 A가 갇히게 되고 위상순서 2가된다.

마지막으로 방문안한 노드 D에서 방문해서, D의 진출간선 종점에 위치하는 정점은 이미 위상순서가 결정되어있으므로
간선을 제거하고 갇히게되어 위상순서 1이 되고 위상정렬이 마무리된다.
위의 과정에서 싸이클을 탐색하는 방법은
방문은 했지만 번호가 안붙어있다면 싸이클이 존재한다는 것이다. (단 이전노드가 아니어야함)

위의 수행 과정을 참고해서 수도코드를 이해하면 잘 이해할 수 있다.

두 위상정렬 알고리즘 분석

'지난 학기들의 기록 > 알고리즘' 카테고리의 다른 글
| [강의노트] 최소신장트리 - 1 (1) | 2021.11.26 |
|---|---|
| [강의노트] 방향그래프 - 1 (0) | 2021.11.17 |
| [강의노트] 그래프 순회 -2 (BFS) (0) | 2021.11.17 |
| [강의노트] 그래프 순회 - 1 (DFS와 싸이클찾기) (0) | 2021.11.10 |
| [강의노트] 무방향 그래프 구현 - 3 (가중치 수정) (0) | 2021.11.07 |




댓글