| 그래프 순회 - 1 |
그래프를 구현하는 문제에 대해서 지난 시간에 해결해보았다.
이번에 배울것은 그래프 순회이다. 깊이우선탐색과 너비우선탐색은 내가 알고리즘을 공부하기전에도
매우 자주 듣던 익숙한 단어이다. 그만큼 중요한 개념이니 꼼꼼하게 공부해두자.
그래프 순회
문제 상황을 그래프로 표현했으면, 그 데이터를 효과적으로 이용하기 위해서는 순회하는 과정이 꼭 필요하다.
그래프를 순회한다는 것은 정점과 간선을 순회한다는 것이므로, 이를 이뤄낼 수 있는 어떤 체계적인 절차가 필요하다.
대표적인 두가지 절차인 깊이우선탐색과 너비우선탐색을 배워보게 된다.

깊이우선탐색(DFS)
먼저 DFS에 대해서 알아보자. DFS 는 depth-first search 의 준말로 그래프를 순회하는 일반적인 기법이다.
DFS순회로 가능한 것들
- G의 모든 정점과 간선을 방문할 수 있다.
- G가 연결그래프인지 아닌지 결정할 수 있다.
- G의 연결요소들을 계산할 수 있다.
- G의 신장숲을 계산할 수 있다.
일반적으로 DFS는 n개의 정점과 m개의 간선을 가진 그래프에 대해 O(n+m)의 시간복잡도를 가진다.
DFS를 확장하면 해결 가능한 그래프 문제들
- 1. 두 개의 주어진 정점 사이의 경로를 찾아 보고하기
- 2. 그래프 내 싸이클 찾기
그래프에 대한 깊이우선탐색은 이진트리의 선위순회와 유사하다.

수도코드에 보면 정점의 상태를 표기하는 것 중 Fresh 라는 말이 나온다. Fresh는 방문하지 않았다는 뜻으로, 초기상태를 의미한다. 방문했으면 Visited로 바뀔 것이다.
즉 정점의 상태는 방문했으면 Visited 방문하지않았으면 Fresh 이다.
간선에는 Fresh와 Tree, Back 세가지 상태가 존재한다. 각각의 의미에 대해서는 후에 자세히 다루게 된다.
깊이우선탐색(DFS) 수행 예시
솔직히 위에 수도코드를 봐도 뭔가 한번에 잘 와닿지가 않는다. 이럴땐 예시를 통해 이해하는게 아주 중요하다.
예시를 천천히 살펴보자.

정점 A에서 출발한다. A의 부착간선리스트들은 종점의 알파벳순에 맞게 정렬되어있으므로
간선(A,B)를 통해 제일 먼저 이동하게 된다. 그럼 정점B에서 재귀호출이 수행된다.
이때 정점B에서 부착간선리스트는 A에 대한 간선이 제일 헤드노드에 위치하겠지만, 이미 방문했으므로 Fresh 상태가 아니다. 따라서 C로 가는 부착간선으로 이동하게 된다.
정점 C에서의 부착간선리스트의 헤드노드는 A로 향하는 간선이고, 간선 (C,A)는 Fresh 상태이므로 A를 확인한다.
이때 C의 반대 정점인 A가 이미 방문한 정점이므로 간선 C,A는 Tree가 아닌 Back 상태가 된다.
주의해야할 것은 이 경우는 정점 A(즉 w노드)에 대한 재귀호출을 수행하지 않는다는 것이다.

그렇게 되면 정점C의 부착간선리스트를 순회하며 Fresh를 체크하다가 간선(C,D)를 찾게된다.
정점D는 Fresh 이므로, 정점 D에서 다시 rDFS가 호출되고 정점D의 부착간선리스트의 헤드노드인 간선(D,A)를 확인한다.
A는 Visited이므로 back , 즉 후향간선으로 표시한다.
이제 D에 대한 재귀호출이 끝났으므로 쭉 되돌아간다. 되돌아가는 과정에서 정점C 에서의 부착간선리스트 E에 대한 간선(C,E)를 확인하고 E는 Fresh 이므로 방문하고 재귀호출을 수행한다. 그 뒤에 정점 E에서 부착간선리스트의 헤드노드 간선(E,A)를 검사하고
A가 방문된 상태이므로 간선을 후향간선으로 표기한다.
결과적으로, 초기 호출 rDFS(G,A)에 대해서 모든 정점과 간선을 방문하게 되었다.
이것을 다른 말로 루트노드(또는 임의의 노드)에서 시작해서 다음 분기로 넘어가기전에 해당 분기를 완벽하게 탐색했다라고 표현한다.
DFS 구현
DFS 를 한번 구현해보자. 아래의 수도코드를 참고했다.
시작 정점 u에 대해서, u의 인접간선의 리스트들을 순회한다.
인접간선 리스트의 끝점이 시작 정점 u에 대한 인접 정점에 해당된다.
번호가 작은 정점부터 큰 순서대로 조사하는 것은 이미 그래프 구현부터 오름차순으로 구현했기때문에 신경쓰지않아도 된다. 위에서 다루었던 트리 간선과 후향 간선에 대한 내용은 수도코드에 포함되어있지않는 것에 주의.

아래는 코드이다.
시작정점 u의 인접간선 리스트의 헤드노드를 adj로 설정한 뒤에
adj를 순회하면서 인접정점을 방문한다. adj->end는 인접간선 adj의 종점을 의미하고
adj의 종점이 방문되지 않은 상태이면 재귀호출을 수행한다.
| void DFS(VERTEX* u) { u->visited = 1; //방문 EDGE* adj = NULL; printf("%d\n", u->data); adj = u->incidenceList; while (adj != NULL) { if (adj->end != NULL && adj->end->visited == 0) { DFS(adj->end); //재귀호출 } adj = adj->next; } } |
한번 예시를 입력해서 수행해보자.
아래의 예시는 n은 정점의 수, m은 간선의 수, s는 시작 정점 번호를 의미한다.
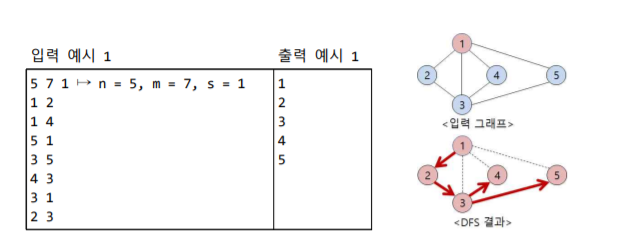
즉 위의 예시 그래프에서, DFS 를 통해 순회하면 1->2->3->4->5 노드 순으로 순회한다는 것이다.
위의 알고리즘을 적용하면 어렵지않게 받아들일 수 있다.
아래의 결과를 통해 생각해볼 것은, 1번 시작노드가 호출되고, 재귀호출과정을 거쳐 모든 노드를 방문하고 마지막이 되어서야 1번노드의 호출이 종료된다. 즉 시작정점에 대한 한번의 호출로 재귀적인 과정을 통해 모든 노드를 순환한 것이다.

이번엔 두번째 예시를 넣어보자.
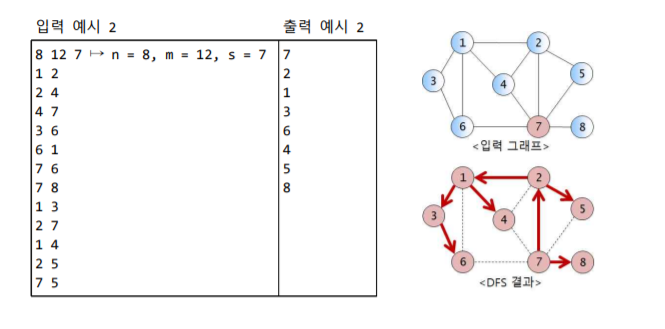

마찬가지로 7번 노드를 시작 정점으로 했을때 한번의 시작노드 호출로 재귀과정을 거쳐 모든 노드를 순환했다.
즉 다시 말하면 정점의 라벨을 읽고 쓰는데 O(1) 시간이 필요하므로, 현재 내가 작성한 코드는 O(n) 시간에 dfs를 수행하고 있다. 만약 간선의 라벨링까지 추가한다면 O(n+m)의 시간에 수행하게 된다.

DFS 를 사용해서 싸이클 존재 여부 판단하기
DFS를 이용하면 해결할 수 있는 문제의 예시중 싸이클 찾기가 있다. DFS를 어떻게 확장해야 싸이클을 찾는 메소드로 바꿀 수 있을까?

아래그래프는 한 눈에 봐도 싸이클이 존재한다는 것을 알 수 있다. 나는 이것을 어떻게 판단하는 것일까?
출발점에서 순회과정을 거쳐 다시 출발점으로 되돌아오는 것을 보고 싸이클이라고 판단한다.
즉 1번 노드를 기준으로 생각하면 여러개의 싸이클이 존재하는데, 알고리즘으로 구현하려면 시작점과 도착점이 1이라는 것을 조건으로 주어야할 것이다. 아래는 예시를 들어본 것이다.
1->2->3->1
1->3->4->1
1->3->5->1
따라서 싸이클을 판단하는 방법은 dfs순회에서 시작노드로 다시 되돌아오는 경우를 찾으면 되는 것이다.
물론 1번 노드는 하나의 예시이고, 모든 노드를 시작정점으로 설정해서 판단해보아야한다.

좀 더 상세하게 싸이클을 판단하는 알고리즘을 설명하면 다음과 같다
1. 정점 u를 시점으로 했을때 다음에 방문해야할 정점은 이미 방문한 정점인 출발점으로 되돌아와야한다
2. 바로 직전에 방문한 정점이 아니어야한다
사이클 판단 수행 결과. (알고리즘은 각자 구현해보자)
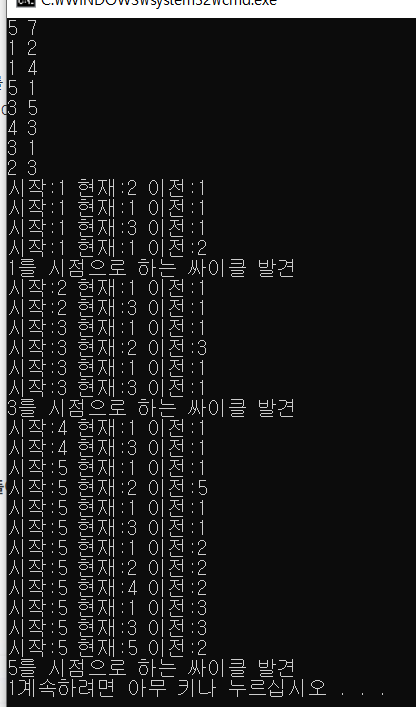
DFS 속성

'지난 학기들의 기록 > 알고리즘' 카테고리의 다른 글
| [강의노트] 방향그래프 - 1 (0) | 2021.11.17 |
|---|---|
| [강의노트] 그래프 순회 -2 (BFS) (0) | 2021.11.17 |
| [강의노트] 무방향 그래프 구현 - 3 (가중치 수정) (0) | 2021.11.07 |
| [강의노트] 무방향 그래프 구현 - 2 (0) | 2021.11.06 |
| [강의노트] 무방향 그래프 - 1 (0) | 2021.11.05 |



댓글